题目内容
已知椭圆C：
的离心率为
，过右焦点F且斜率为1的直线交椭圆C于A、B两点，N为弦AB的中点.
（Ⅰ）求直线ON（O为坐标原点）的斜率
；
（Ⅱ）对于椭圆C上任意一点M，试证：对任意的
等式
都成立.
解：（Ⅰ）∵离心率为
∴
∴
∴椭圆方程为
， ∴F的坐标为
∴AB：
与联立得：
设
， 
， 
∴
， 
∴
………………………………………………………………6分
（Ⅱ）由（Ⅰ）知
， 
由平面向量基本定理得：存在实数
、
，使
成立.
若设
∴
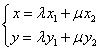……………………………………8分
∵M在椭圆上，∴
即：
由（Ⅰ）
=
， 
=
+
=
∴ 
=1……………………………………………………………10分
令
，则
∴总存在角
（∈R）使
成立……………12分
练习册系列答案
相关题目
的离心率为
，双曲线x²-y²＝1的渐近线与椭圆有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆c的方程为
的离心率为
，且经过点
．
的离心率为
，过右焦点
且斜率为
的直线与椭圆C相交于
、
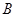两点．若
，则
=( ) 
B．
C．2
D．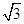
,它的离心率为
.直线
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
的离心率为
，椭圆C上任意一点到椭圆两个焦点的距离之和为6．
：
与椭圆C交于
，
两点，点
，且
，求直线