题目内容
19.两圆x2+y2+2ax+a2-4=0和x2+y2-4by-1+4b2=0恰有三条公切线,则a+2b的最大值为3$\sqrt{2}$.分析 由题意可得两圆相外切,根据两圆的标准方程求出圆心和半径,可得a2+4b2=9,再利用三角换元,求a+2b的最大值.
解答 解:由题意可得两圆相外切,两圆的标准方程分别为 (x+a)2+y2=4,x2+(y-2b)2=1,
圆心分别为(-a,0),(0,2b),半径分别为2和1,故有$\sqrt{{a}^{2}+4{b}^{2}}$=3,∴a2+4b2=9,
设a=3cosα,b=$\frac{3}{2}$sinα,
∴a+2b=3cosα+3sinα=3$\sqrt{2}$sin(α+$\frac{π}{4}$),
∴sin(α+$\frac{π}{4}$)=1时,a+2b的最大值为3$\sqrt{2}$
故答案为:3$\sqrt{2}$.
点评 本题考查两圆的位置关系,两圆相外切的性质,圆的标准方程的特征,得到a2+4b2=9是解题的关键和难点.

练习册系列答案
相关题目
7.已知m,n均为正数,曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1过定点A(1,$\sqrt{2}$),则m+n的最小值是( )
| A. | 2($\sqrt{2}$+1) | B. | 4$\sqrt{2}$ | C. | ($\sqrt{2}$+1)2 | D. | 4($\sqrt{2}$+1)2 |
14.下列命题中为真命题的是( )
| A. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| B. | 若直线x-ay=0与直线x+ay=0互相垂直,则a=1 | |
| C. | 命题“若x2=1,则x=1或x=-1”的逆否命题为“若x≠1且x≠-1,则x2≠1” | |
| D. | 一个命题的否命题为真,则它的逆否命题一定为真 |
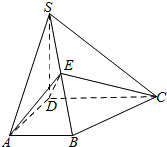 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.