题目内容
在周长为定值的△ABC中,已知AB=6,且当顶点C位于定点P时,cosC有最小值为 .
.
(Ⅰ)建立适当的坐标系,求顶点C的轨迹方程;
(Ⅱ)(理)过点A作直线与(Ⅰ)中的曲线交于M,N两点,求|BM|•|BN|的最小值的集合.
(文)当点Q在(Ⅰ)中的曲线上运动时,求|PQ|的最大值的集合.
解:(Ⅰ)以AB所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,设PA+PB=2a(a>0)为定值,所以P点的轨迹是以A、B为焦点的椭圆,∴焦距2c=AB=6 (1分)
∵ (2分)
(2分)
又∵PB.PA ,
, ,此时p(0,±4),由题意得
,此时p(0,±4),由题意得
∴a2=25∴C点的轨迹方程为 (3分)
(3分)
(注:y≠0没写扣(1分):文科(Ⅰ)分别为2,3,(3分),共8分)
(Ⅱ)(理)设M(x1,y1),N(x2,y2 ),
当直线MN的倾斜角不为90°时,设其方程为y=k(x+3)代入椭圆方程化简得 ,显然有△≥0
,显然有△≥0
∴x1+x2=- ,x1.x2=
,x1.x2=
而由椭圆第二定义可得|BM|•|BN|=(5- )(5-
)(5- )=25-3(x1+x2)
)=25-3(x1+x2)  …(2分)
…(2分)
=25+
只考虑 的最小值,即考虑1-
的最小值,即考虑1- 的最小值,易知当k=0时,1-
的最小值,易知当k=0时,1- 的最小值
的最小值
此时|BM|•|BN|取最小值16(2分)
当直线MN的倾斜角为90°时,x1=x2=-3得|BM|•|BN|=(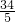 )2>16;(1分)
)2>16;(1分)
但 ,故这样的M,N不存在,即|BM|•|BN|的最小值集合为空集(1分)
,故这样的M,N不存在,即|BM|•|BN|的最小值集合为空集(1分)
(文)由(Ⅰ)知P(0,±4,)不妨取P(0,4),
则|PQ|2=x2+(y-4)2=25- +(y-4)2=-
+(y-4)2=- ,
,
∵-4≤y≤4且y≠0,
∴当y=-4时,|PQ|取到最大值8 集合为{8} (6分)
分析:(Ⅰ)P点的轨迹是以A、B为焦点的椭圆,2c=AB,由余弦定理可得 及基本不等式PB.PA
及基本不等式PB.PA ,可求
,可求 ,从而可求a,及C点的轨迹方程
,从而可求a,及C点的轨迹方程
(Ⅱ)(理)设M(x1,y1),N(x2,y2 ),设其方程为y=k(x+3)代入椭圆方程化简 ,显然有△≥0,由椭圆第二定义可得|BM|•|BN|=(5-
,显然有△≥0,由椭圆第二定义可得|BM|•|BN|=(5- )(5-
)(5- )及方程的根与系数的关系|BM|•|BN|取最小值,结合椭圆的
)及方程的根与系数的关系|BM|•|BN|取最小值,结合椭圆的 得性质判断M,N是否存在,使得|BM|•|BN|的最小值
得性质判断M,N是否存在,使得|BM|•|BN|的最小值
(文)由(Ⅰ)知P(0,±4,)不妨取P(0,4),则|PQ|2=x2+(y-4)2=25- +(y-4)2
+(y-4)2
=- ,由-4≤y≤4且y≠0,结合二次函数的性质可求
,由-4≤y≤4且y≠0,结合二次函数的性质可求
点评:本题主要考查了利用椭圆的性质及余弦定理求解椭圆的方程,利用函数的性质求解函数的最值问题,要求考试具备一定的逻辑推理与运算的能力
∵
 (2分)
(2分)又∵PB.PA
 ,
, ,此时p(0,±4),由题意得
,此时p(0,±4),由题意得
∴a2=25∴C点的轨迹方程为
 (3分)
(3分)(注:y≠0没写扣(1分):文科(Ⅰ)分别为2,3,(3分),共8分)
(Ⅱ)(理)设M(x1,y1),N(x2,y2 ),
当直线MN的倾斜角不为90°时,设其方程为y=k(x+3)代入椭圆方程化简得
 ,显然有△≥0
,显然有△≥0∴x1+x2=-
 ,x1.x2=
,x1.x2=
而由椭圆第二定义可得|BM|•|BN|=(5-
 )(5-
)(5- )=25-3(x1+x2)
)=25-3(x1+x2)  …(2分)
…(2分)=25+

只考虑
 的最小值,即考虑1-
的最小值,即考虑1- 的最小值,易知当k=0时,1-
的最小值,易知当k=0时,1- 的最小值
的最小值此时|BM|•|BN|取最小值16(2分)
当直线MN的倾斜角为90°时,x1=x2=-3得|BM|•|BN|=(
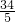 )2>16;(1分)
)2>16;(1分)但
 ,故这样的M,N不存在,即|BM|•|BN|的最小值集合为空集(1分)
,故这样的M,N不存在,即|BM|•|BN|的最小值集合为空集(1分)(文)由(Ⅰ)知P(0,±4,)不妨取P(0,4),
则|PQ|2=x2+(y-4)2=25-
 +(y-4)2=-
+(y-4)2=- ,
,∵-4≤y≤4且y≠0,
∴当y=-4时,|PQ|取到最大值8 集合为{8} (6分)
分析:(Ⅰ)P点的轨迹是以A、B为焦点的椭圆,2c=AB,由余弦定理可得
 及基本不等式PB.PA
及基本不等式PB.PA ,可求
,可求 ,从而可求a,及C点的轨迹方程
,从而可求a,及C点的轨迹方程(Ⅱ)(理)设M(x1,y1),N(x2,y2 ),设其方程为y=k(x+3)代入椭圆方程化简
 ,显然有△≥0,由椭圆第二定义可得|BM|•|BN|=(5-
,显然有△≥0,由椭圆第二定义可得|BM|•|BN|=(5- )(5-
)(5- )及方程的根与系数的关系|BM|•|BN|取最小值,结合椭圆的
)及方程的根与系数的关系|BM|•|BN|取最小值,结合椭圆的 得性质判断M,N是否存在,使得|BM|•|BN|的最小值
得性质判断M,N是否存在,使得|BM|•|BN|的最小值(文)由(Ⅰ)知P(0,±4,)不妨取P(0,4),则|PQ|2=x2+(y-4)2=25-
 +(y-4)2
+(y-4)2=-
 ,由-4≤y≤4且y≠0,结合二次函数的性质可求
,由-4≤y≤4且y≠0,结合二次函数的性质可求点评:本题主要考查了利用椭圆的性质及余弦定理求解椭圆的方程,利用函数的性质求解函数的最值问题,要求考试具备一定的逻辑推理与运算的能力

练习册系列答案
相关题目
 ,动点C的运动轨迹为曲线G,且当动点C运动时,
,动点C的运动轨迹为曲线G,且当动点C运动时, 有最小值
有最小值 .
. (其中
(其中 )于A、B两点,求|AB|的取值范围.
)于A、B两点,求|AB|的取值范围.