题目内容
设
=(sin2
,cosx-sinx),
=(4cosx,cosx+sinx),f(x)=
•
.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)+2
|sinx|,x∈[0,2π]的图象与直线y=k有且仅有四个不同的交点,求实数k的取值范围.
| a |
| x |
| 2 |
| b |
| a |
| b |
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)+2
| 3 |
分析:(1)利用两个向量数量积的公式求得f(x)的解析式.
(2)根据函数g(x)=f(x)+2
|sinx|=
,画出函数g(x)的图象,数形结合求得k的范围.
(2)根据函数g(x)=f(x)+2
| 3 |
|
解答:解:(1)f(x)=
•
=4cosxsin2
+cos2x-sin2x=2cosx-1.
(2)函数g(x)=f(x)+2
|sinx|=2cosx+2
|sinx|-1=
,
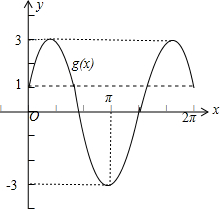
画出函数g(x)的图象,如图:
故当函数g(x)的图象与直线y=k有且仅有四个不同的交点时,k的范围为[1,3).
| a |
| b |
| x |
| 2 |
(2)函数g(x)=f(x)+2
| 3 |
| 3 |
|
画出函数g(x)的图象,如图:
故当函数g(x)的图象与直线y=k有且仅有四个不同的交点时,k的范围为[1,3).

点评:本题主要考查两个向量的数量积公式,方程根的存在性及个数判断,体现了转化、和数形结合的数学思想,
属于中档题.
属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
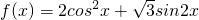 ,
,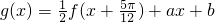 ,其中a,b为非零实常数.
,其中a,b为非零实常数.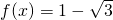 ,
,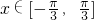 ,求x;
,求x;