题目内容
已知数列{an}中, ,则数列{an}的最大项是第________项.
,则数列{an}的最大项是第________项.
12、13
分析:由数列的通项公式 ,我们利用函数求最值的方法及基本不等式求出数列的最大项,但要注意数列中自变量n∈N+的限制.
,我们利用函数求最值的方法及基本不等式求出数列的最大项,但要注意数列中自变量n∈N+的限制.
解答:∵ =
= ≤
≤
∵ ≤
≤ 当且仅当n=
当且仅当n=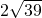 时取等,
时取等,
又由n∈N+,
故数列{an}的最大项可能为第12项或第13项
又∵当n=12时, =
=
又∵当n=13时, =
=
故第12项或第13项均为最大项,
故答案为:12、13.
点评:本题考查的知识点是数列的函数特征,其中根据数列{an}的通项,将求数列的最大项转化为求函数的最大值问题,是解答本题的关键.
分析:由数列的通项公式
 ,我们利用函数求最值的方法及基本不等式求出数列的最大项,但要注意数列中自变量n∈N+的限制.
,我们利用函数求最值的方法及基本不等式求出数列的最大项,但要注意数列中自变量n∈N+的限制.解答:∵
 =
= ≤
≤
∵
 ≤
≤ 当且仅当n=
当且仅当n=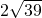 时取等,
时取等,又由n∈N+,
故数列{an}的最大项可能为第12项或第13项
又∵当n=12时,
 =
=
又∵当n=13时,
 =
=
故第12项或第13项均为最大项,
故答案为:12、13.
点评:本题考查的知识点是数列的函数特征,其中根据数列{an}的通项,将求数列的最大项转化为求函数的最大值问题,是解答本题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|