题目内容

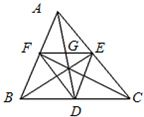精英家教网如图，在△ABC中，D、E、F分别是各边的中点，AD交EF于点G，则下列各式能表示向量
DG
的有①
1
2
(
DE
+
DF
)，②
1
2
(
CF
+
BE
)，③
1
2
(
BF
+
CE
)，④-
1
4
(
AB
+
AC
)（　　）
A、1个B、2个C、3个D、4个
分析：先由D、E、F分别是各边的中点，得出四边形AFDE是平行四边形，根据向量加法的平行四边形法则得出①正确；②③④两式均可能利用向量加法的三角形法则转化为①，从而即可判断它们的正确性．
解答：解：∵D、E、F分别是各边的中点，
∴四边形AFDE是平行四边形，
∴
DG
=
1
2
(
DE
+
DF
)，①正确；
∵
1
2
(
CF
+
BE
)=
1
2
(
CD
+
DF
+
BD
+
DE
)=
1
2
(
DE
+
DF
)，故②正确；
1
2
(
BF
+
CE
)=
1
2
(
BE
+
EF
+
CF
+
FE
)=
1
2
(
CF
+
BE
)，故③正确；
-
1
4
(
AB
+
AC
)=-
1
2
(
AF
+
AE
)=
1
2
(
DE
+
DF
)，故④正确．
故选D．
点评：本题主要考查了平面向量的基本定理、向量加法的平行四边形法则和三角形法则，解答的关键是灵活应用这两个法则表示向量．
练习册系列答案
相关题目
精英家教网如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
AD=4cm．
（1）求：⊙O的直径BE的长；
（2）计算：△ABC的面积．
精英家教网如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
3
BD，BC=2BD，则sinC的值为（　　）
A、
3
3
B、
3
6
C、
6
3
D、
6
6
如图，在△ABC中，设
AB
=a，
AC
=b，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
（Ⅰ）若
AP
=λa+μb，求λ和μ的值；
（Ⅱ）以AB，AC为邻边，AP为对角线，作平行四边形ANPM，求平行四边形ANPM和三角形ABC的面积之比
S平行四边形ANPM
S△ABC
．
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
（1）求∠ADC的大小；
（2）求AB的长．
如图，在△ABC中，已知
BD
=2
DC
，则
AD
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网