题目内容
已知函数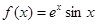 .
.
(Ⅰ)求函数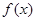 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的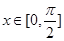 ,
,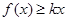 总成立,求实数
总成立,求实数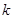 的取值范围;
的取值范围;
(Ⅲ)是否存在正实数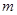 ,使得:当
,使得:当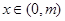 时,不等式
时,不等式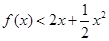 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由.
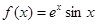 .
.(Ⅰ)求函数
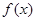 的单调区间;
的单调区间;(Ⅱ)如果对于任意的
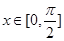 ,
,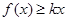 总成立,求实数
总成立,求实数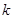 的取值范围;
的取值范围;(Ⅲ)是否存在正实数
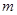 ,使得:当
,使得:当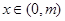 时,不等式
时,不等式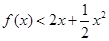 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由.(Ⅰ)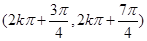 ;(Ⅱ)
;(Ⅱ)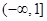 ;(Ⅲ)存在,
;(Ⅲ)存在,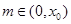 .
.
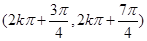 ;(Ⅱ)
;(Ⅱ)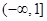 ;(Ⅲ)存在,
;(Ⅲ)存在,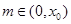 .
.试题分析:(Ⅰ)先求
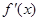 ,利用辅助角公式,函数
,利用辅助角公式,函数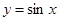 的性质求得;(Ⅱ)构造新函数,用导数法求解,需要对
的性质求得;(Ⅱ)构造新函数,用导数法求解,需要对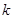 进行分类讨论;(Ⅲ)探索性问题,构造新函数
进行分类讨论;(Ⅲ)探索性问题,构造新函数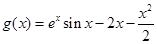 ,用导数法解题.
,用导数法解题.试题解析:(Ⅰ)由于
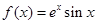 ,
,所以
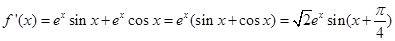 . (2分)
. (2分)当
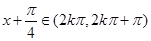 ,即
,即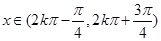 时,
时,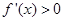 ;
;当
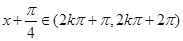 ,即
,即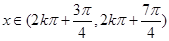 时,
时,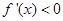 .
.所以
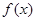 的单调递增区间为
的单调递增区间为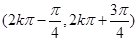
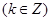 ,
,单调递减区间为
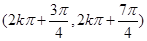
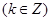 . (4分)
. (4分)(Ⅱ)令
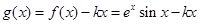 ,要使
,要使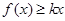 总成立,只需
总成立,只需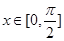 时
时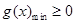 .
.对
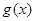 求导得
求导得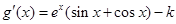 ,
,令
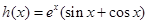 ,则
,则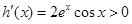 ,(
,(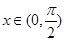 )
)所以
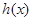 在
在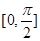 上为增函数,所以
上为增函数,所以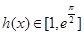 . (6分)
. (6分)对
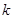 分类讨论:
分类讨论:① 当
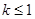 时,
时,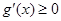 恒成立,所以
恒成立,所以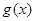 在
在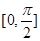 上为增函数,
上为增函数,所以
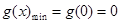 ,即
,即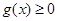 恒成立;
恒成立;② 当
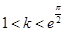 时,
时,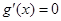 在上有实根
在上有实根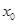 ,因为
,因为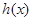 在
在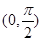 上为增函数,
上为增函数,所以当
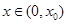 时,
时,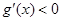 ,所以
,所以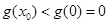 ,不符合题意;
,不符合题意;③ 当
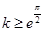 时,
时,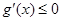 恒成立,所以
恒成立,所以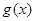 在
在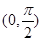 上为减函数,则
上为减函数,则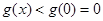 ,不符合题意.
,不符合题意. 综合①②③可得,所求的实数
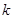 的取值范围是
的取值范围是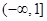 . (9分)
. (9分)(Ⅲ)存在正实数
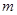 使得当
使得当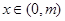 时,不等式
时,不等式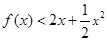 恒成立.
恒成立. 理由如下:令
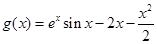 ,要使
,要使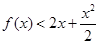 在
在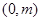 上恒成立,只需
上恒成立,只需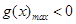 . (10分)
. (10分)因为
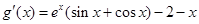 ,且
,且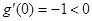 ,
,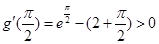 ,
,所以存在正实数
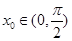 ,使得
,使得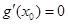 ,
,当
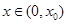 时,
时,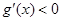 ,
,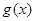 在
在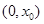 上单调递减,即当
上单调递减,即当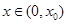 时,
时,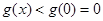 ,
,所以只需
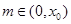 均满足:当
均满足:当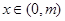 时,
时,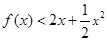 恒成立. (14分)
恒成立. (14分)注:因为
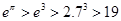 ,
,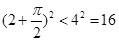 ,所以
,所以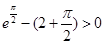
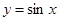 的性质,恒成立问题.
的性质,恒成立问题.
练习册系列答案
相关题目
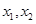 是关于
是关于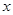 的方程
的方程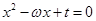 的两个根,且
的两个根,且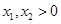 .
.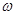 与
与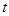 之间满足的关系式;
之间满足的关系式;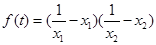 ,若存在
,若存在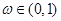 ,使不等式
,使不等式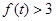 在其定义域范围内恒成立,求
在其定义域范围内恒成立,求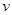 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度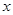 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到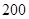 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当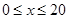 时,车流速度为
时,车流速度为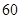 千米/小时.研究表明:当
千米/小时.研究表明:当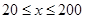 时,车流速度
时,车流速度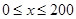 时,求函数
时,求函数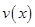 的表达式;
的表达式;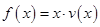 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)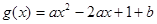 (
(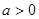 )在区间
)在区间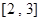 上有最大值
上有最大值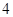 和最小值
和最小值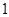 .设
.设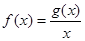 .
.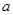 、
、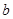 的值;
的值;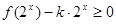 在
在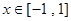 上有解,求实数
上有解,求实数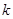 的取值范围.
的取值范围.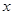 的方程
的方程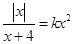 有四个不同的实数解,则
有四个不同的实数解,则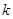 的取值范围为 ( )
的取值范围为 ( )



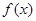 满足
满足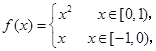 且
且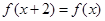 ,
,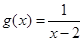 ,则方程
,则方程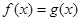 在区间
在区间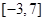 上的所有实根之和最接近下列哪个数( )
上的所有实根之和最接近下列哪个数( )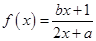 ,其中
,其中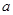 、
、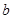 为常数,且
为常数,且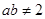 ,若
,若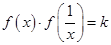 为常数,则
为常数,则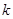 的值为 .
的值为 .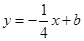 是函数
是函数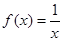 的切线,则实数
的切线,则实数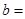 .
.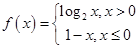 ,则
,则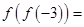 ___________.
___________.