题目内容
(2013•汕头二模)已知函数f(x)=Asin(ωx+φ)(A,ω>0,|φ|<
)的图象与y轴交于(0,3
),它在y右侧的第一个最高点和第一个最低点的坐标分别为(m,6)和(m+
,-6).
(1)求函数f(x)的解析式及m的值;
(2)若锐角θ满足tanθ=2
,求f(θ).
| π |
| 2 |
| 2 |
| π |
| 2 |
(1)求函数f(x)的解析式及m的值;
(2)若锐角θ满足tanθ=2
| 2 |
分析:(1)由图象的最高点的纵坐标求A,由周期求ω,把点(0,3
)代入函数的解析式求得φ,从而求得函数解析式,再根据函数在y右侧的第一个最高点的坐标
为(m,6),可得2m+
=
,由此解得 m的值.
(2)由条件利用同角三角函数的基本关系求得sinθ 和cosθ 的值,再利用两角和差正弦公式、二倍角公式求得f(θ)=6sin(2θ+
) 的值.
| 2 |
为(m,6),可得2m+
| π |
| 4 |
| π |
| 2 |
(2)由条件利用同角三角函数的基本关系求得sinθ 和cosθ 的值,再利用两角和差正弦公式、二倍角公式求得f(θ)=6sin(2θ+
| π |
| 4 |
解答:解:(1)由函数的图象在y右侧的第一个最高点和第一个最低点的坐标分别为(m,6)和(m+
,-6),可得A=6,
•T=
•
=(m+
)-m=
,求得ω=2.
把点(0,3
)代入函数的解析式可得 6sin(2×0+φ)=3
,解得sinφ=
,再由|φ|<
,求得φ=
.
故f(x)=6sin(2x+
).
函数在y右侧的第一个最高点的坐标分别为(m,6),故2m+
=
,解得 m=
.
(2)若锐角θ满足tanθ=2
,θ∈(0,
),∴sinθ=
,cosθ=
.
f(θ)=6sin(2θ+
)=6sin2θ•cos
+6cos2θ•sin
=6
sinθcosθ+3
(2cos2θ-1)
=6
×
×
+3
(2×
-1)=
.
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 2 |
| π |
| 2 |
把点(0,3
| 2 |
| 2 |
| ||
| 2 |
| π |
| 2 |
| π |
| 4 |
故f(x)=6sin(2x+
| π |
| 4 |
函数在y右侧的第一个最高点的坐标分别为(m,6),故2m+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
(2)若锐角θ满足tanθ=2
| 2 |
| π |
| 2 |
2
| ||
| 3 |
| 1 |
| 3 |
f(θ)=6sin(2θ+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 2 |
=6
| 2 |
2
| ||
| 3 |
| 1 |
| 3 |
| 2 |
| 1 |
| 9 |
8-7
| ||
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,两角和差正弦公式、二倍角公式、同角三角函数的基本关系,求函数的值,属于中档题.

练习册系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为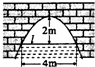 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽