题目内容
已知f(x)=x(x-a)(x-b),点A(s,f(s)),B(t,f(t)).
(1)若a=b=1,求函数f(x)的单调递增区间;
(2)若函数f(x)的导函数![]() 满足:当|x|≤1时,有
满足:当|x|≤1时,有![]()
![]() 恒成立,求函数f(x)的解析表达式;
恒成立,求函数f(x)的解析表达式;
(3)若0<a<b,函数f(x)在x=s和x=t处取得极值,且a+b=![]() ,证明:
,证明:![]() 与
与![]() 不可能垂直.
不可能垂直.
答案:
解析:
解析:
解:(Ⅰ)![]() ,
,![]()
令![]() 得
得![]() ,解得
,解得![]()
故![]() 的增区间
的增区间![]() 和
和![]()
(Ⅱ)![]() (x)=
(x)=![]()
当x∈[-1,1]时,恒有|![]() (x)|≤
(x)|≤![]() . 4分
. 4分
故有![]() ≤
≤![]() (1)≤
(1)≤![]() ,
,![]() ≤
≤![]() (-1)≤
(-1)≤![]() ,
,
及![]() ≤
≤![]() (0)≤
(0)≤![]() , 5分
, 5分
即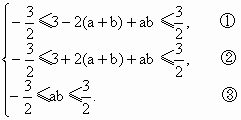 6分
6分
①+②,得![]() ≤
≤![]() ≤
≤![]() , 8分
, 8分
又由③,得![]() =
=![]() ,将上式代回①和②,得
,将上式代回①和②,得![]()
故![]()
![]() . 9分
. 9分
(Ⅲ)假设![]() ⊥
⊥![]() ,
,
即![]()
![]() =
=![]() 10分
10分
故(s-a)(s-b)(t-a)(t-b)=-1
[st-(s+t)a+a2][st-(s+t)b+b2]=-1, 11分
由s,t为![]() (x)=0的两根可得,s+t=
(x)=0的两根可得,s+t=![]() (a+b),st=
(a+b),st=![]() ,(0<a<b)
,(0<a<b)
从而有ab(a-b)2=9. 12分
这样![]()
即![]() ≥2
≥2![]() ,这与
,这与![]() <2
<2![]() 矛盾. 13分
矛盾. 13分
故![]() 与
与![]() 不可能垂直. 14分
不可能垂直. 14分

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

