题目内容

1．某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，事件A表示“2名学生全不是男生”，事件B表示“2名学生全是男生”，事件C表示“2名学生中至少有一名是男生”，则下列结论中正确的是（　　）
A．A与B对立B．A与C对立
C．B与C互斥D．任何两个事件均不互斥

分析 利用互斥事件、对立事件的定义求解．

解答 解：某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，
事件A表示“2名学生全不是男生”，事件B表示“2名学生全是男生”，事件C表示“2名学生中至少有一名是男生”，
∴A与B不能同时发生，但能同时不发生，故A与B是互斥但不对立事件，故A和D都错误；
A与C不能同时发生，也不能同时不发生，故A与C是对立事件，故B正确；
B与C能同时发生，故B与C不是互斥事件，故C错误．
故选：B．

点评 本题考查对立事件、互斥事件的判断，是基础题，解题时要熟练掌握基本概念．

练习册系列答案
相关题目
11．椭圆C的中心在坐标原点，焦点在x轴上，焦点到短轴端点的距离为2，离心率为$\frac{\sqrt{3}}{2}$．
（Ⅰ）求该椭圆的方程；
（Ⅱ）若直线l与椭圆C交于A，B两点且OA⊥OB，是否存在以原点O为圆心的定圆与直线l相切？若存在求出定圆方程；若不存在，请说明理由．
12．已知F1，F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点，点A是椭圆的右顶点，O为坐标原点，若椭圆上的一点M满足MF1⊥MF2，|MA|=|MO|，则椭圆的离心率为（　　）
A．$\frac{\sqrt{10}}{5}$B．$\frac{2}{3}$C．$\frac{\sqrt{2}}{2}$D．$\frac{2\sqrt{7}}{7}$
9．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点与抛物线C2：x2=4y的焦点重合，F1、F2分别是椭圆C1的左、右焦点，C1的离心率e=$\frac{\sqrt{2}}{2}$，过F2的直线l与椭圆C1交于M，N两点，与抛物线C2交于P，Q两点．
（1）求椭圆C1的方程；
（2）当直线l的斜率k=-1时，求△PQF1的面积；
（3）在x轴上是否存在点A，$\overrightarrow{AM}$•$\overrightarrow{AN}$为常数？若存在，求出点A的坐标和这个常数；若不存在，请说明理由．
16．在△ABC中a，b，c分别为角A，B，C的对边，且$\sqrt{3}$bcosA=asinB
（Ⅰ）求角A
（Ⅱ）若a=2$\sqrt{3}$，求bc的最大值．
6．已知直线l1：2x-my=1，l2：（m-1）x-y=1，若l1∥l2，则实数m的值为2或-1．
13．设a=0.61.6，b=0.61.5，c=1.50.6，则a，b，c的大小关系是（　　）
A．a＜b＜cB．b＜c＜aC．b＜a＜cD．c＜b＜a
10．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的半焦距为c，且b=c，椭圆的上顶点到右顶点的距离为2$\sqrt{3}$．
（1）求椭圆的方程；
（2）已知点F是椭圆的右焦点，C（m，0）是线段OF上一个动点（O为坐标原点），是否存在过点F且与x轴不垂直的直线l与椭圆交于A，B两点，使得AC|=|BC|，并说明理由．
11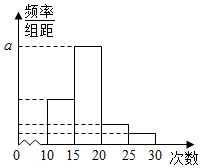．对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组频数频率
[10，15）100.25
[15，20）25n
[20，25）mp
[25，30）20.05
合计M1
（1）求出表中M、p及图中a的值；
（2）试估计他们参加社区服务的平均次数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至少1人参加社区服务次数在区间[20，25）内的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网