Question

12．已知F₁，F₂分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点，点A是椭圆的右顶点，O为坐标原点，若椭圆上的一点M满足MF₁⊥MF₂，|MA|=|MO|，则椭圆的离心率为（　　）

• A． $\frac{\sqrt{10}}{5}$
• B． $\frac{2}{3}$
• C． $\frac{\sqrt{2}}{2}$
• D． $\frac{2\sqrt{7}}{7}$

Answer 1

分析 过M作MN⊥x轴，交x轴于N，不妨设M在第一象限，从而得到M（$\frac{a}{2}$，$\frac{\sqrt{3}}{2}b$），由此利用MF₁⊥MF₂，能求出椭圆的离心率．

解答 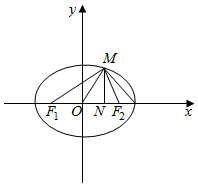解：∵F₁，F₂分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点，点A是椭圆的右顶点，O为坐标原点，
椭圆上的一点M满足MF₁⊥MF₂，|MA|=|MO|，
过M作MN⊥x轴，交x轴于N，不妨设M在第一象限，
∴N是OA的中点，∴M点横坐标为$\frac{a}{2}$，∴M点纵坐标为$\frac{\sqrt{3}}{2}b$，
∴F₁（-c，0），F₂（c，0），${S}_{△M{F}_{1}{F}_{2}}$=$\frac{1}{2}×2c×\frac{\sqrt{3}}{2}b$=$\frac{\sqrt{3}}{2}bc$，
$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$=（$\frac{a}{2}+c$，$\frac{\sqrt{3}}{2}b$）•（$\frac{a}{2}-c，\frac{\sqrt{3}}{2}b$）=$\frac{{a}^{2}}{4}-{c}^{2}+\frac{3}{4}{b}^{2}$=0，
∴4c²=a²+3b²=a²+3a²-3c²，∴4a²=7c²，∴2a=$\sqrt{7}c$，
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{2\sqrt{7}}{7}$．
故选：D．

点评 本题考查椭圆的离心率的求法，是中档题，解题时要认真审题，注意直线垂直的性质的合理运用．