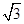题目内容
如图，
是圆柱的母线，
是圆柱底面圆的直径，
是底面圆周上异于
的任意一点，
.（Ⅰ）求证:
平面
；（Ⅱ）求三棱锥
的体积的最大值.
是圆柱的母线，是圆柱底面圆的直径，是底面圆周上异于的任意一点，.（Ⅰ）求证:平面；（Ⅱ）求三棱锥的体积的最大值.(I)证明: ∵C是底面圆周上异于A，B的任意一点，且AB是圆柱底面圆的直径，∴BC⊥AC, ∵AA1⊥平面ABC，BCÌ平面ABC，∴AA1⊥BC，
∵AA1∩AC=A，AA1Ì平面AA1 C，ACÌ平面AA1 C，
∴BC⊥平面AA1C. --------------------6分
(Ⅱ)解：设AC=x，在Rt△ABC中，
(0<x<2) ,
故
(0<x<2),
即
.
∵0<x<2，0<x2<4，∴当x2=2，
即
时，三棱锥A1-ABC的体积的最大值为
.
∵AA1∩AC=A，AA1Ì平面AA1 C，ACÌ平面AA1 C，
∴BC⊥平面AA1C. --------------------6分
(Ⅱ)解：设AC=x，在Rt△ABC中，
(0<x<2) , 故
(0<x<2), 即
. ∵0<x<2，0<x2<4，∴当x2=2，
即
时，三棱锥A1-ABC的体积的最大值为.略
练习册系列答案
相关题目
的长方形，左视图是边长为2的等边三角形，俯视图如图所示，则这个几何体的体积为 （ ）
，那么原△ABC是一个( ) 
