题目内容
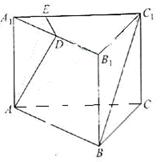
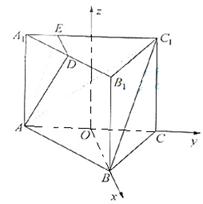
如图4,在正三棱柱![]() 中,
中,![]()
D是![]() 的中点,点E在
的中点,点E在![]() 上,且
上,且![]() 。
。
(I) 证明平面![]() 平面
平面![]()
(II) 求直线![]() 和平面
和平面![]() 所成角的正弦值。
所成角的正弦值。![]()
![]()
(Ⅰ)略(Ⅱ)![]()
解析:
(I) 如图所示,由正三棱柱![]() 的性质知
的性质知![]() 平面
平面![]()
又DE![]() 平面A
平面A![]() B
B![]() C
C![]() ,所以DE
,所以DE![]() AA
AA![]() .
.
而DE![]() AE。AA
AE。AA![]()
![]() AE=A 所以DE
AE=A 所以DE![]() 平面AC C
平面AC C![]() A
A![]() ,又DE
,又DE![]() 平面ADE,故平面ADE
平面ADE,故平面ADE![]() 平面AC C
平面AC C![]() A
A![]() 。
。
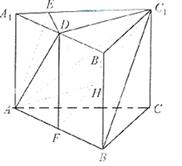
(2)解法1 如图所示,设F使AB的中点,连接DF、DC、CF,由正三棱柱ABC- A![]() B
B![]() C
C![]() 的性质及D是A
的性质及D是A![]() B的中点知A
B的中点知A![]() B
B![]() C
C![]() D, A
D, A![]() B
B![]() DF
DF![]()
![]()
又C![]() D
D![]() DF=D,所以A
DF=D,所以A![]() B
B![]() 平面C
平面C![]() DF,
DF,
而AB∥A![]() B,所以
B,所以
AB![]() 平面C
平面C![]() DF,又AB
DF,又AB![]() 平面ABC,故
平面ABC,故
平面AB C![]()
![]() 平面C
平面C![]() DF。
DF。
过点D做DH垂直C![]() F于点H,则DH
F于点H,则DH![]() 平面AB C
平面AB C![]() 。
。![]()
![]()
连接AH,则![]() HAD是AD和平面ABC
HAD是AD和平面ABC![]() 所成的角。
所成的角。
由已知AB=![]() A A
A A![]() ,不妨设A A
,不妨设A A![]() =
=![]() ,则AB=2,DF=
,则AB=2,DF=![]() ,D C
,D C![]() =
=![]() ,
,
C![]() F=
F=![]() ,AD=
,AD=![]() =
=![]() ,DH=
,DH=![]() =
=![]() —
—![]() ,
,
所以 sin![]() HAD=
HAD=![]() =
=![]() 。
。
即直线AD和平面AB C![]() 所成角的正弦值为
所成角的正弦值为![]() 。
。
解法2 如图所示,设O使AC的中点,以O为原点建立空间直角坐标系,不妨设
A A![]() =
=![]() ,则AB=2,相关各点的坐标分别是
,则AB=2,相关各点的坐标分别是
A(0,-1,0), B(![]() ,0,0), C
,0,0), C![]() (0,1,
(0,1,![]() ), D(
), D(![]() ,-
,-![]() ,
,![]() )。
)。
易知![]() =(
=(![]() ,1,0),
,1,0), ![]() =(0,2,
=(0,2,![]() ),
), ![]() =(
=(![]() ,-
,-![]() ,
,![]() )
)![]()
![]()
设平面ABC![]() 的法向量为n=(x,y,z),则有
的法向量为n=(x,y,z),则有
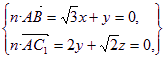
解得x=-![]() y, z=-
y, z=-![]() ,
,
故可取n=(1,-![]() ,
,![]() )。
)。
所以,![]() (n·
(n·![]() )=
)=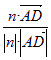 =
=![]() =
=![]() 。
。
由此即知,直线AD和平面AB C![]() 所成角的正弦值为
所成角的正弦值为![]() 。
。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目


 (2009湖南卷理)(本小题满分12分)
(2009湖南卷理)(本小题满分12分)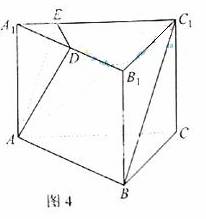 (2009湖南卷理)(本小题满分12分)
(2009湖南卷理)(本小题满分12分)