题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() 位于抛物线
位于抛物线![]() 上.
上.
(1)求抛物线![]() 的方程;
的方程;
(2)设抛物线![]() 的准线与其对称轴的交点为
的准线与其对称轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,
, ![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,求直线
,求直线![]() 所过的定点.
所过的定点.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设![]() ,则
,则![]() ,进而解得坐标带入抛物线即可得解;
,进而解得坐标带入抛物线即可得解;
(2)根据题意, ![]() ,设点
,设点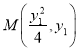 ,
,  ,由
,由![]() ,利用坐标运算得
,利用坐标运算得![]() ,设点
,设点 ,由
,由![]() ,得
,得![]() ,利用点斜式得直线
,利用点斜式得直线![]() 的方程是
的方程是 ,代入条件整理可得
,代入条件整理可得![]() ,从而证得过定点
,从而证得过定点![]() .
.
试题解析:
(1)设![]() ,则
,则![]() ,∴
,∴![]() ,解之得
,解之得![]() ,
,
代入![]() ,得
,得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() .
.
(2)根据题意, ![]() ,设点
,设点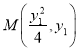 ,
,  ,
,
因为![]() ,
, ![]() ,
, ![]() 三点共线,
三点共线,
所以![]() ,即
,即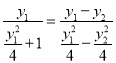 ,∴
,∴![]() ,∴
,∴![]() ,
,
设点 ,因为
,因为![]() ,
, ![]() ,
, ![]() 三点共线,
三点共线,
所以![]() ,即
,即 ,∴
,∴![]() .
.
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ①,
①,
因为 ,所以直线
,所以直线![]() 的方程是
的方程是 .
.
即![]() ,即
,即![]() ②,
②,
由①②可得![]() .所以直线
.所以直线![]() 过定点
过定点![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目