Question

【题目】如图，在梯形中，，，四边形

为矩形，平面平面，.

（I）求证：平面；

（II）点在线段上运动，设平面与平面所成二面角的平面角为，

试求的取值范围.

Answer 1

【答案】(1)详见解析；(2).

【解析】

(1)由题意结合勾股定理和余弦定理可证得BC⊥AC，结合面面垂直的性质定理可得BC⊥平面ACFE.

(2)以CA,CB,CF所在的直线为x轴,y轴,z轴建立空间直角坐标系,由题意可得平面MAB的一个法向量n1=(1,,-λ)，平面FCB的一个法向量n2=(1,0,0)，则 cosθ=，结合三角函数的性质可得cosθ∈[,].

(1)在梯形ABCD中,∵AB∥CD,AD=DC=CB=1,∠ABC=60°,

∴AB=2,∴AC2=AB2+BC2-2AB·BC·cos 60°=3,

∴AB2=AC2+BC2,∴BC⊥AC.

又平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,BC平面ABCD,

∴BC⊥平面ACFE.

(2)由(1)知,可分别以CA,CB,CF所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,

令FM=λ(0≤λ≤),则C(0,0,0),A(,0,0),B(0,1,0),M(λ,0,1),

∴=(-,1,0),=(λ,-1,1).

设n1=(x,y,z)为平面MAB的法向量,

由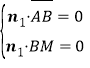,得,

取x=1,则n1=(1,,-λ)为平面MAB的一个法向量,

易知n2=(1,0,0)是平面FCB的一个法向量,

∴ cosθ=.

∵0≤λ≤, ∴当λ=0时,cosθ有最小值, 当λ=时,cosθ有最大值,∴cosθ∈[,].