题目内容
12．如图，PA⊥平面ABC，∠ABC=90°且PA=AC=BC=a，则异面直线PB与AC所成角的正切值等于_______.
|
12.
解法一：如下图所示，过B作BD
AC，
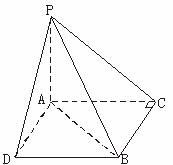
则四边形ACBD为矩形.
∴∠PBD是异面直线PB与AC所成角的平面角，连结PD.
∵BD⊥AD，∴BD⊥PD.
又∵BD=AC=a，PD=
a，
∴tan∠PBD=
=
.
解法二：分别取PA、PC、BC的中点为D、E、F，连结DE、EF、DF、AF.
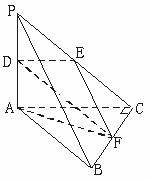
∵DE∥AC，EF∥PB，
∴∠DEF是异面直线AC与PB所成角的平面角.
∴DE=
，EF=
=
，DF=
=
=
=
a.
∴cos∠DEF=
=
=－
，
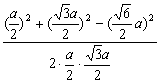∴tan∠DEF=
.
练习册系列答案
活力课时同步练习册系列答案
相关题目
如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，M，N分别是AB，PC的中点．
如图，PA⊥平面AC，四边形ABCD是矩形，E、F分别是AB、PD的中点．
如图，PA⊥平面ABC，AC⊥BC，AB=2，
（2010•天津模拟）如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，PD与平面ABCD所成的角是30°，点
如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AB=1，PD与平面ABCD所成的角是30°，点F是PB的中点，点E在边BC上移动．