题目内容
点M是曲线C上任意一点,它到F(4,0)的距离比它到直线x+2=0的距离大2,且P(2m,m)(m>0),A(x1,y1),B(x2,y2)均在曲线C上.
(1)写出该曲线C的方程及 m的值;
(2)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
(1)写出该曲线C的方程及 m的值;
(2)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
分析:(1)由题意,根据圆锥曲线的定义可知曲线C为以F为焦点的抛物线,从而可求其方程,把点P代入方程可得m;
(2)由(1)知P(64,32),由PA,PB倾斜角互补且斜率存在,得kPA+kPB=0,代入斜率公式后转化纵坐标的方程可求y1+y2,再由斜率公式可求AB斜率;
(2)由(1)知P(64,32),由PA,PB倾斜角互补且斜率存在,得kPA+kPB=0,代入斜率公式后转化纵坐标的方程可求y1+y2,再由斜率公式可求AB斜率;
解答:解:(1)由题意:M是曲线C上任意一点,它到F(4,0)的距离比它到直线x+2=0的距离大2,
因此,它到F(4,0)的距离等于它到直线x+4=0的距离,
根据圆锥曲线的定义可知,曲线C为抛物线,且以F(4,0)为其焦点,
设y2=2px,
=4,2p=16,
∴曲线C的方程为y2=16x,
又P(2m,m)在曲线C上,∴m2=32m,解得m=32;
(2)由(1)知P(64,32),
∵PA,PB倾斜角互补且斜率存在,∴kPA+kPB=0,
则
+
=0,得
+
=0,即
+
=0,
∴y2+32+y1+32=0,∴y1+y2=-64,
kAB=
=
=
=
=-
.
因此,它到F(4,0)的距离等于它到直线x+4=0的距离,
根据圆锥曲线的定义可知,曲线C为抛物线,且以F(4,0)为其焦点,
设y2=2px,
| p |
| 2 |
∴曲线C的方程为y2=16x,
又P(2m,m)在曲线C上,∴m2=32m,解得m=32;
(2)由(1)知P(64,32),
∵PA,PB倾斜角互补且斜率存在,∴kPA+kPB=0,
则
| y1-32 |
| x1-64 |
| y2-32 |
| x2-64 |
| y1-32 | ||
|
| y2-64 | ||
|
| 16 |
| y1+32 |
| 16 |
| y2+32 |
∴y2+32+y1+32=0,∴y1+y2=-64,
kAB=
| y2-y1 |
| x2-y1 |
| y2-y1 | ||||
|
| 16 |
| y1+y2 |
| 16 |
| -64 |
| 1 |
| 4 |
点评:本题考查直线与圆锥曲线的位置关系、直线的斜率公式,考查学生分析解决问题的能力,有一定运算量.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
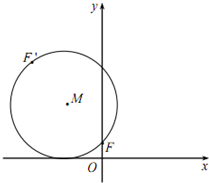 (2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
(2012•深圳二模)如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.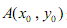 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q.