题目内容
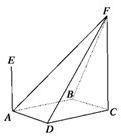
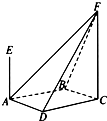 如图所示,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=
如图所示,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=| 2 |
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
分析:(1)连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG,根据定义可知∠BGD为二面角B-AF-D的平面角,在三角形BGD中求出此角即可;
(2)连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD,过H作HP⊥平面ABCD,P为垂足,然后求出HP,利用体积公式V=
S菱形ABCD•HP求解即可.
(2)连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD,过H作HP⊥平面ABCD,P为垂足,然后求出HP,利用体积公式V=
| 1 |
| 3 |
解答:解:(1)解:连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG.
由BD⊥AC,BD⊥CF得BD⊥平面ACF,故BD⊥AF.
于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角.
由FC⊥AC,FC=AC=2,得∠FAC=
,OG=
.
由OB⊥OG,OB=OD=
,得∠BGD=2∠BGO=
.
(2)解:连接EB、EC、ED,设直线AF与直线CE相交于点H,
则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD.
过H作HP⊥平面ABCD,P为垂足.
因为EA⊥平面ABCD,FC⊥平面ABCD,
所以平面ACEF⊥平面ABCD,从而P∈AC,HP⊥AC.
由
+
=
+
=1,得HP=
.
又因为S菱形ABCD=
AC•BD=
,
故四棱锥H-ABCD的体积V=
S菱形ABCD•HP=
.
由BD⊥AC,BD⊥CF得BD⊥平面ACF,故BD⊥AF.
于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角.
由FC⊥AC,FC=AC=2,得∠FAC=
| π |
| 4 |
| ||
| 2 |
由OB⊥OG,OB=OD=
| ||
| 2 |
| π |
| 2 |
(2)解:连接EB、EC、ED,设直线AF与直线CE相交于点H,
则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD.
过H作HP⊥平面ABCD,P为垂足.
因为EA⊥平面ABCD,FC⊥平面ABCD,
所以平面ACEF⊥平面ABCD,从而P∈AC,HP⊥AC.
由
| HP |
| CF |
| HP |
| AE |
| AP |
| AC |
| PC |
| AC |
| 2 |
| 3 |
又因为S菱形ABCD=
| 1 |
| 2 |
| 2 |
故四棱锥H-ABCD的体积V=
| 1 |
| 3 |
2
| ||
| 9 |
点评:本题考查空间位置关系,二面角平面角的作法以及空间几何体的体积计算等知识.考查利用综合法或向量法解决立体几何问题的能力.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
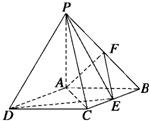 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,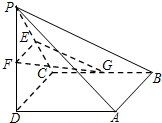 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.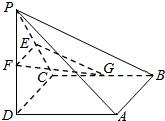 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2,E、F、G分别为PC、PD、BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2,E、F、G分别为PC、PD、BC的中点.