题目内容
8．若曲线y=x2-ax+1在点P（0，1）处的切线方程为x-y+1=0，则实数a的值为（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 求出函数的导数，求得切线的斜率，由切线的方程可得a的方程，可得a=-1．
解答 解：y=x2-ax+1的导数为y′=2x-a，
在点P（0，1）处的切线斜率为k=-a，
由切线的方程x-y+1=0，可得-a=1，解得a=-1．
故选：A．
点评 本题考查导数的运用：求切线的斜率，考查导数的几何意义，正确求导和直线方程的运用是解题的关键，属于基础题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
19．若函数f（x）的定义域为（-4，4），函数f（2x）的定义域为集合A，集合B={x|x2-x+a-a2＜0}，其中a＜0．
（1）若A∪B=B，求a的取值范围；
（2）若A∩B=B，求a的取值范围．
（1）若A∪B=B，求a的取值范围；
（2）若A∩B=B，求a的取值范围．
16．
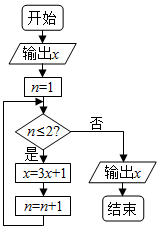从1，2，3，4，5，6，7，8中随机取出一个数为x，执行如图所示的程序框图，则输出的x不小于40的概率为（ ）
从1，2，3，4，5，6，7，8中随机取出一个数为x，执行如图所示的程序框图，则输出的x不小于40的概率为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{5}{8}$ | C． | $\frac{7}{8}$ | D． | $\frac{1}{2}$ |
3．从$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{n}=1$（m，n∈{-1，2，3}）所表示的圆锥曲线（椭圆、双曲线）方程中任取一个，则此方程是焦点在x轴上的双曲线方程的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{4}{7}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
20．从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表如下：
（I）用分层抽样的方法从重量在[80，85）和[90，95）的苹果中共抽取5个，其中重量在[90，85）的有几个？
（Ⅱ）在（I）中抽出的5个苹果中，任取2个，求重量在[80，85）和[90，95）中各有1个的概率．
| 分组（重量） | [80，85） | [85，90） | [90，95） | [95，100） |
| 频数（个） | 5 | 10 | 20 | 15 |
（Ⅱ）在（I）中抽出的5个苹果中，任取2个，求重量在[80，85）和[90，95）中各有1个的概率．
18．已知命题p：菱形的对角线相等；命题q：矩形对角线互相垂直．下面四个结论中正确的是（ ）
| A． | p∧q是真命题 | B． | p∨q是真命题 | C． | ￢p是真命题 | D． | ￢q是假命题 |