题目内容
设a为实数,f(x)=(x2+
)(x+a)
1)若y=f(x)有平行于x轴的切线,求实数a的取值范围
2)若f′(-1)=0,①求y=f(x)的单调区间;②任意实数x1,x2∈[-1,0],不等式:|f(x1)-f(x2)|≤m恒成立,求实数m的最小值.
| 3 | 2 |
1)若y=f(x)有平行于x轴的切线,求实数a的取值范围
2)若f′(-1)=0,①求y=f(x)的单调区间;②任意实数x1,x2∈[-1,0],不等式:|f(x1)-f(x2)|≤m恒成立,求实数m的最小值.
分析:(1)根据求导公式和法则求出导数,再由题意得f′(x)=0有解,根据判别式与方程的根关系,列出不等式求出a的范围;
(2)由f′(-1)=0求出a的值,代入由f′(x),求出临界点,f′(x)≥0和f′(x)≤0解集,即求出函数单调区间,再求出[-1,0]上的最大值和最小值,根据条件和恒成立对最大值和最小值作差,求出m的范围,再求出m的最小值.
(2)由f′(-1)=0求出a的值,代入由f′(x),求出临界点,f′(x)≥0和f′(x)≤0解集,即求出函数单调区间,再求出[-1,0]上的最大值和最小值,根据条件和恒成立对最大值和最小值作差,求出m的范围,再求出m的最小值.
解答:解:(1)由题意得,f′(x)=(x2+
)′(x+a)+(x2+
)(x+a)′
=2x(x+a)+x2+
=3x2+2ax+
,
∵y=f(x)有平行于x轴的切线,
∴f′(x)=3x2+2ax+
=0有解,即△=4a2-4×3×
≥0,
即a2≥
,解得a≥
或a≤-
,
(2)由f′(-1)=0得,3-2a+
=0,解得a=
,
∴f′(x)=3x2+2ax+
=3x2+
x+
,
由f′(x)=0得,3x2+
x+
=0,解得x=-1或-
,
由f′(x)≥0得,x≤-1或x≥-
,
由f′(x)≤0得,-1≤x≤-
,
∴函数的增区间是(-∞,-1),(-
,+∞),
减区间是[-1,-
],
则任意实数x1,x2∈[-1,0],
当x=-
时,函数取最小值f(-
)=(
+
)(-
+
)=
,
∵f(0)=(0+
)(0+
)=
,f(-1)=(1+
)(-1+
)=
,
∴当x=-1时,函数取最大值
,
∵|f(x1)-f(x2)|≤m恒成立,
∴m≥
-
=
,
故实数m的最小值是
.
| 3 |
| 2 |
| 3 |
| 2 |
=2x(x+a)+x2+
| 3 |
| 2 |
| 3 |
| 2 |
∵y=f(x)有平行于x轴的切线,
∴f′(x)=3x2+2ax+
| 3 |
| 2 |
| 3 |
| 2 |
即a2≥
| 9 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
(2)由f′(-1)=0得,3-2a+
| 3 |
| 2 |
| 9 |
| 4 |
∴f′(x)=3x2+2ax+
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
由f′(x)=0得,3x2+
| 9 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
由f′(x)≥0得,x≤-1或x≥-
| 1 |
| 2 |
由f′(x)≤0得,-1≤x≤-
| 1 |
| 2 |
∴函数的增区间是(-∞,-1),(-
| 1 |
| 2 |
减区间是[-1,-
| 1 |
| 2 |
则任意实数x1,x2∈[-1,0],
当x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 49 |
| 16 |
∵f(0)=(0+
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
| 3 |
| 2 |
| 9 |
| 4 |
| 25 |
| 8 |
∴当x=-1时,函数取最大值
| 27 |
| 8 |
∵|f(x1)-f(x2)|≤m恒成立,
∴m≥
| 27 |
| 8 |
| 49 |
| 16 |
| 5 |
| 16 |
故实数m的最小值是
| 5 |
| 16 |
点评:本题考查了导数的几何意义,利用导数研究函数单调性和最值,以及恒成立求参数的范围,此类问题一般用导数解决,综合性较强.

练习册系列答案
相关题目
 (x∈R).
(x∈R).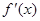 ,且
,且