题目内容
如图2-24:B为![]() ACD所在平面外一点,M、N、G分别为
ACD所在平面外一点,M、N、G分别为![]() ABC、
ABC、![]() ABD、
ABD、![]() BCD的重心,
BCD的重心,
(1)求证:平面MNG//平面ACD;
(2)求![]()

解析:
(1)要证明平面MNG//平面ACD,由于M、N、G分别
为△ABC、△ABD、△BCD的重心,因此可想到利用重心的性
质找出与平面平行的直线。
证明:连结BM、BN、BG并延长交AC、AD、CD分别于P、F、H。
∵M、N、G分别为△ABC、△ABD、△BCD的重心,
则有:![]()
连结PF、FH、PH有MN∥PF,又PF![]() 平面ACD,∴MN∥平面ACD。
平面ACD,∴MN∥平面ACD。
同理:MG∥平面ACD,MG∩MN=M,
∴平面MNG∥平面ACD
(2)分析:因为△MNG所在的平面与△ACD所在的平面相互平行,因此,求两三角形的面积之比,实则求这两个三角形的对应边之比。
解:由(1)可知![]() ,
,
∴MG=![]() PH,又PH=
PH,又PH=![]() AD,∴MG=
AD,∴MG=![]() AD
AD
同理:NG=![]() AC,MN=
AC,MN=![]() CD,
CD,
∴![]() MNG∽
MNG∽![]() ACD,其相似比为1:3,
ACD,其相似比为1:3,
∴![]() =1:9
=1:9
点评:立体几何问题,一般都是化成平面几何问题,所以要重视平面几何。比如重心定理,三角形的三边中线交点叫做三角形有重心,到顶点的距离等于它到对边中点距离的2倍。

练习册系列答案
相关题目
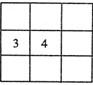 12、将1,2,3,,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大,当3,4固定在图中的位置时,填写空格的方法数为( )
12、将1,2,3,,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大,当3,4固定在图中的位置时,填写空格的方法数为( ) 5、如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
5、如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( ) 春节期间,某地昼夜气温呈周期性变化,温度y随时间x变化近似满足函数y=Asin(ωx+?)+b(A>0,ω>0,-π<?≤π)(如图4),且在每天凌晨2时达到最低温度-3℃,在下午14时达到最高温度9℃.
春节期间,某地昼夜气温呈周期性变化,温度y随时间x变化近似满足函数y=Asin(ωx+?)+b(A>0,ω>0,-π<?≤π)(如图4),且在每天凌晨2时达到最低温度-3℃,在下午14时达到最高温度9℃. (2013•茂名二模)已知某几何体的三视图如图,其中正视图中半圆半径为1,则该几何体体积为 ( )
(2013•茂名二模)已知某几何体的三视图如图,其中正视图中半圆半径为1,则该几何体体积为 ( )
 B.24+
B.24+ D.32+
D.32+