题目内容
先后抛掷两枚骰子,计算:(1)共有多少种不同的结果?
(2)其中向上数字之和是5的有多少种?
(3)出现点数相同的概率.
(4)出现的点数和为奇数的概率.
(5)出现点数和为奇数且先奇后偶的概率.
(6)若抛掷三枚骰子,则出现点数都相同的概率为多少?
(7)若以连续投掷两枚骰子分别得到的点数m、n作为点P的坐标(m,n),求点P落在圆x2+y2=16内的概率.
解析:抛掷骰子的问题是典型的等可能性问题,每一面的数字向上的可能性是相等的.
(1)先后抛掷两枚骰子得到的不同结果,即基本事件总数是6×6=36个.?
(2)有(1,4),(2,3),(3,2),(4,1)四种情况.?
(3)设点数相同的事件为A1,则A1包含以下6个基本事件:(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),则P(A1)=![]() .?
.?
(4)设两次出现的点数和为奇数的事件为A2,则A2包含2
 =18个基本事件(先奇后偶或先偶后奇两种情况),则?
=18个基本事件(先奇后偶或先偶后奇两种情况),则?
P(A2)=![]() .?
.?
另法:由于向上的点数不是奇数就是偶数,且每个点数出现的可能性相等,则两枚骰子点数之和为奇数或偶数的可能性也相等,各为![]() .?
.?
(5)设两次出现的点数为先奇后偶的事件为A3,则由(4)便知A3包含
 =9个基本事件,则P(A3)=
=9个基本事件,则P(A3)=![]() .?
.?
(6)若抛掷三枚骰子,出现点数相同的事件为A4,则出现的结果共有n=6×6×?6=?216个,点数相同的结果m= =6,则?
=6,则?
P(A4)=![]() .?
.?
(7)点(m,n),m\,n∈{1,2,3,4,5,6},共有6×6=36种,P(m,n)落在圆x2+y2=16内的点有8个:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),则?
P(A)=![]() .
.

练习册系列答案
相关题目
 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程 实根的个数(重根按一个计).
实根的个数(重根按一个计).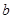 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量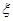 表示方程
表示方程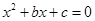 实根的个数(重根按一个计).
实根的个数(重根按一个计).