题目内容
已知 是3a与3b的等比中项,且a,b∈R+,则
是3a与3b的等比中项,且a,b∈R+,则 的最小值为
的最小值为
- A.4
- B.2
- C.3
- D.1
A
分析:依题意,可求得a+b=1,a,b∈R+,利用基本不等式即可求得 +
+ 的最小值.
的最小值.
解答:∵ 是3a与3b的等比中项,
是3a与3b的等比中项,
∴3a•3b=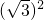 =31,
=31,
∴a+b=1,
又a,b∈R+,
∴ +
+ =(
=( +
+ )•(a+b)=1+1+
)•(a+b)=1+1+ +
+ ≥4.(当且仅当a=b=1时取“=”).
≥4.(当且仅当a=b=1时取“=”).
∴ +
+ 的最小值是4.
的最小值是4.
故选A.
点评:本题考查基本不等式,依题意求得a+b=1是关键,属于基础题.
分析:依题意,可求得a+b=1,a,b∈R+,利用基本不等式即可求得
 +
+ 的最小值.
的最小值.解答:∵
 是3a与3b的等比中项,
是3a与3b的等比中项,∴3a•3b=
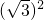 =31,
=31,∴a+b=1,
又a,b∈R+,
∴
 +
+ =(
=( +
+ )•(a+b)=1+1+
)•(a+b)=1+1+ +
+ ≥4.(当且仅当a=b=1时取“=”).
≥4.(当且仅当a=b=1时取“=”).∴
 +
+ 的最小值是4.
的最小值是4.故选A.
点评:本题考查基本不等式,依题意求得a+b=1是关键,属于基础题.

练习册系列答案
相关题目
 是3a与3b的等比中项,且a,b∈R+,则
是3a与3b的等比中项,且a,b∈R+,则 的最小值为( )
的最小值为( ) 是3a与3b的等比中项,且a,b∈R+,则
是3a与3b的等比中项,且a,b∈R+,则 的最小值为( )
的最小值为( ) 是3a与3b的等比中项,其中a,b>0,则
是3a与3b的等比中项,其中a,b>0,则 的最小值为 .
的最小值为 .