Question

（本题满分14分）

已知半径为的圆的圆心在轴上，圆心的横坐标是整数，且与直线相切．

（1）求圆的方程；

（2）设直线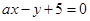与圆相交于两点，求实数的取值范围；

（3） 在（2）的条件下，是否存在实数，使得弦的垂直平分线过点，若存在，求出实数的值；若不存在，请说明理由．

 

Answer 1

【答案】

（1）；

（2）；

（3）存在实数使得过点的直线垂直平分弦AB

【解析】(1)设圆心M（m,0）,根据圆与直线4x+3y-29=0相切，半径为5,可建立关于m的方程，求出m的值1.

（2）利用圆心到直线的距离小于半径建立关于a的不等式求解即可.

（3）设符合条件的实数存在，由于直线l与直线AB垂直，则直线的斜率为

的方程为，即

由于垂直平分弦AB，故圆心必在上，据此可建立关于a的方程，通过方程是否有解再结合（2）求的a的取值范围，判定a值是否存在.

解：（Ⅰ）设圆心为（）．由于圆与直线相切，且半径为，所以 ，即．因为为整数，故．

故所求圆的方程为． …………………………………4分

 （Ⅲ）设符合条件的实数存在，由于，则直线的斜率为

的方程为，即

由于垂直平分弦AB，故圆心必在上，

所以，解得.由于，故存在实数

使得过点的直线垂直平分弦AB………………………14分