题目内容
已知数列 中,
中, ,对任意的
,对任意的 ,
, 、
、 、
、 成等比数列,公比为
成等比数列,公比为 ;
; 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,且
,且 .
.
(1)写出数列 的前四项;
的前四项;
(2)设 ,求数列
,求数列 的通项公式;
的通项公式;
(3)求数列 的前
的前 项和
项和 .
.
 中,
中, ,对任意的
,对任意的 ,
, 、
、 、
、 成等比数列,公比为
成等比数列,公比为 ;
; 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,且
,且 .
.(1)写出数列
 的前四项;
的前四项;(2)设
 ,求数列
,求数列 的通项公式;
的通项公式;(3)求数列
 的前
的前 项和
项和 .
.(1) 或
或 ;(2)
;(2) 或
或 ;(3)
;(3) 时,
时, ,
, 时,
时, .
.
 或
或 ;(2)
;(2) 或
或 ;(3)
;(3) 时,
时, ,
, 时,
时, .
.试题分析:(1)求数列的前4项,相对较容易,由题意可得
 成等比数列,而
成等比数列,而 ,要求得
,要求得 ,对应再求得
,对应再求得 ;(2)要求
;(2)要求 ,实质上就是求
,实质上就是求 ,我们应求出
,我们应求出 的递推关系,从而求出通项,由题意
的递推关系,从而求出通项,由题意 ,
, ,而
,而 ,这样就有
,这样就有 ,于是关于
,于是关于 的递推关系就有了:
的递推关系就有了: ,把它变形或用
,把它变形或用 代入就可得到结论;(3)由(2)我们求出了
代入就可得到结论;(3)由(2)我们求出了 ,下面为了求
,下面为了求 ,我们要把数列
,我们要把数列 从前到后建立一个关系,分析已知,发现
从前到后建立一个关系,分析已知,发现 ,这样就由
,这样就由 而求出
而求出 ,于是
,于是 ,
, ,得到数列
,得到数列 的通项公式后,其前
的通项公式后,其前 项和也就可求得了. 另外由于第(1)题中已知求出的数列
项和也就可求得了. 另外由于第(1)题中已知求出的数列 的前4项(我们还可再求出接下来的一些项,增强想象),然后用猜想的方法猜测出其通项公式(
的前4项(我们还可再求出接下来的一些项,增强想象),然后用猜想的方法猜测出其通项公式( ),再数学归纳法证明之.
),再数学归纳法证明之. 试题解析:(1)由题意得
 ,
, ,
, 或
或 . 2分
. 2分故数列
 的前四项为
的前四项为 或
或 . 4分
. 4分(2)∵
 成公比为
成公比为 的等比数列,
的等比数列, 成公比为
成公比为 的等比数列
的等比数列∴
 ,
,
又∵
 成等差数列,
成等差数列,∴
 .
.得
 ,
, , 6分
, 6分 ,
,∴
 ,
, ,即
,即 .
.∴ 数列数列
 为公差
为公差 等差数列,且
等差数列,且 或
或 . 8分
. 8分∴
 或
或 . 10分
. 10分(3)当
 时,由(2)得
时,由(2)得 .
. ,
, ,
, ,
, . 13分
. 13分当
 时,同理可得
时,同理可得 ,
, . 16分
. 16分解法二:(2)对
 这个数列,猜想
这个数列,猜想 , 下面用数学归纳法证明:
, 下面用数学归纳法证明:ⅰ)当
 时,
时, ,结论成立.
,结论成立. ⅱ)假设
 时,结论成立,即
时,结论成立,即 .
.则
 时,
时,由归纳假设,
 . 由
. 由 成等差数列可知
成等差数列可知 ,于是
,于是 ,
,∴
 时结论也成立.
时结论也成立.所以由数学归纳法原理知
 . 7分
. 7分此时
 .
.同理对
 这个数列,同样用数学归纳法可证
这个数列,同样用数学归纳法可证 . 此时
. 此时 .
.∴
 或
或 . 10分
. 10分(3)对
 这个数列,猜想奇数项通项公式为
这个数列,猜想奇数项通项公式为 .
.显然结论对
 成立. 设结论对
成立. 设结论对 成立,考虑
成立,考虑 的情形.
的情形.由(2),
 且
且 成等比数列,
成等比数列,故
 ,即结论对
,即结论对 也成立.
也成立.从而由数学归纳法原理知
 .于是
.于是 (易见从第三项起每项均为正数)以及
(易见从第三项起每项均为正数)以及 ,此时
,此时 . 13分
. 13分对于
 这个数列,同样用数学归纳法可证
这个数列,同样用数学归纳法可证 ,此时
,此时 .
.此时
 . 16分
. 16分
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 中的
中的 、
、 、
、 .
. ,求证:数列
,求证:数列 是等比数列.
是等比数列. 中,
中, .
. 是等比数列,并求
是等比数列,并求 ;
; 满足
满足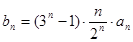 ,数列
,数列 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围. 满足
满足 ,
, ,(
,( )
) ,数列
,数列 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围; ,试写出
,试写出 对任意
对任意 成立的充要条件,并证明你的结论.
成立的充要条件,并证明你的结论. 是各项均不为零的
是各项均不为零的 (
( )项等差数列,且公差
)项等差数列,且公差 .
. ,且该数列前
,且该数列前 最大,求
最大,求 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值; ,则数列
,则数列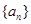 是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。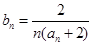 ,求数列
,求数列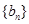 的前
的前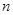 项和
项和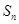
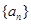 的前
的前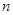 项和为
项和为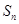 ,且满足
,且满足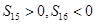 ,则
,则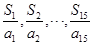 中最大的项为( )
中最大的项为( )


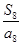
 中的最大项是第
中的最大项是第 项,则
项,则 ( )
( ) ,
, ,以
,以 表示
表示 的前
的前 项和,则使得
项和,则使得