题目内容
已知动圆C过点A(-2,0),且与圆M:(x-2)2+y2=64相内切.
(1)求动圆C的圆心的轨迹方程;
(2)设直线l:y=kx+m(其中k,m∈Z与(1)中所求轨迹交于不同两点B,D,与双曲线![]() 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量![]() ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
答案:
解析:
解析:
|
解:(1)圆 ∵ 设动圆C的半径为r,圆心为C,依题意得r=|CA|,且 即 ∴圆心C的轨迹是中心在原点,以A,M两点为焦点,长轴长为8的椭圆,设其方程为 ∴所求动圆C的圆心的轨迹方程为 (2)由 设 Δ 由 设 Δ ∵ ∴ 当k=0时,由①、②得 ∵m∈Z,∴m的值为 当m=0,由①、②得 ∵k∈Z,∴ ∴满足条件的直线共有9条.12分 |

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 消去y化简整理得:
消去y化简整理得: 消去y化简整理得:
消去y化简整理得: 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 相内切。
相内切。 :
y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线
:
y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线 交于不同两点E,F,问是否存在直线
交于不同两点E,F,问是否存在直线 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.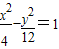 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.