题目内容
已知动圆C过点A(-2,0),且与圆M:(x-2)2+x2=64相内切
(1)求动圆C的圆心的轨迹方程;
(2)设直线l: y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
解:(1)圆M:(x-2)2+x2=64,圆心M的坐标为(2,0),半径R=8.
∵|AM|=4<R,∴点A(-2,0)在圆M内,
设动圆C的半径为r,圆心为C,依题意得r= |CA|,且|CM|=R-r,
即|CM+|CA|=8>|AM|, ……3分
∴圆心CD的轨迹是中心在原点,以A,M两点为焦点,长轴长为8的椭圆,设其方程为 (a>b>0),则a=4,c=2,
(a>b>0),则a=4,c=2,
∴b2=a2-c2=12,
∴所求动圆C的圆心的轨迹方程为 .…5分
.…5分
(2)由 消去y 化简整理得:(3+4k2)x2+8kmx+4m2-48=0,
消去y 化简整理得:(3+4k2)x2+8kmx+4m2-48=0,
设B(x1,y1),D(x2,y2),则x1+x2= .
.
△1=(8km)2-4(3+4k2) (4m2-48)>0. ① ……7分
由 消去y 化简整理得:(3-k2)x2-2kmx-m2-12=0,
消去y 化简整理得:(3-k2)x2-2kmx-m2-12=0,
设E(x3,y3),F(x4,y4),则x3+x4= .
.
△2=(-2km)2+4(3-4k2) (m2+12)>0. ② ……9分
∵ ,∴ (x4-x2 )+ (x3-x1) =0,即x1+x2=
x3+x4,
,∴ (x4-x2 )+ (x3-x1) =0,即x1+x2=
x3+x4,
∴ ,∴2km=0或
,∴2km=0或 ,
,
解得k=0或m=0, ……12分
当k=0时,由①、②得 ,
,
∵m∈Z,∴m的值为-3,-2,-1,0,1,2,3;
当m=0时,由①、②得 ,∵k∈Z,∴k=-1,0,1.
,∵k∈Z,∴k=-1,0,1.
∴满足条件的直线共有9条. ……14分
【解析】略

 相内切。
相内切。 :
y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线
:
y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线 交于不同两点E,F,问是否存在直线
交于不同两点E,F,问是否存在直线 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.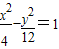 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.