题目内容
在椭圆 +y2=1上求一点M,使点M到直线
+y2=1上求一点M,使点M到直线 (t为参数)的距离最小,并求出该最小距离.
(t为参数)的距离最小,并求出该最小距离.
【答案】分析:设点M(3cosθ,sinθ),0≤θ<2π,直线即 x- y-10=0,求得点M到直线的距离d=|
y-10=0,求得点M到直线的距离d=| cos(θ+
cos(θ+ )-5|,可得当θ=0时,|
)-5|,可得当θ=0时,| cos(θ+
cos(θ+ )-5|取得最小值,从而求得M的坐标.
)-5|取得最小值,从而求得M的坐标.
解答:解:设点M(3cosθ,sinθ),0≤θ<2π,直线 (t为参数)即 x-
(t为参数)即 x- y-10=0,
y-10=0,
点M到直线的距离d= =
= =|
=| cos(θ+
cos(θ+ )-5|,
)-5|,
显然,当θ=0时,| cos(θ+
cos(θ+ )-5|取得最小值为5-
)-5|取得最小值为5- ,此时,M(3,0).
,此时,M(3,0).
点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式,余弦函数的定义域和值域,属于中档题.
 y-10=0,求得点M到直线的距离d=|
y-10=0,求得点M到直线的距离d=| cos(θ+
cos(θ+ )-5|,可得当θ=0时,|
)-5|,可得当θ=0时,| cos(θ+
cos(θ+ )-5|取得最小值,从而求得M的坐标.
)-5|取得最小值,从而求得M的坐标.解答:解:设点M(3cosθ,sinθ),0≤θ<2π,直线
 (t为参数)即 x-
(t为参数)即 x- y-10=0,
y-10=0,点M到直线的距离d=
 =
= =|
=| cos(θ+
cos(θ+ )-5|,
)-5|,显然,当θ=0时,|
 cos(θ+
cos(θ+ )-5|取得最小值为5-
)-5|取得最小值为5- ,此时,M(3,0).
,此时,M(3,0).点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式,余弦函数的定义域和值域,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
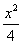 +y2=1上,p=
+y2=1上,p=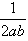 ,求证:点Q落在双曲线4x2-4y2=1上;
,求证:点Q落在双曲线4x2-4y2=1上;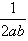 ,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。
,若点Q始终落在一条关于x轴对称的抛物线上,试问动点P的轨迹落在哪种二次曲线上,并说明理由。