题目内容
（1）已知函数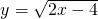
（x≥2），求它的反函数．
（2）根据函数单调性的定义，证明函数f（x）=-x2+1在区间[0，+∞）上是减函数．
解：（1）∵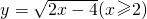
，
∴y2=2x-4，（y≥0），
∴
，
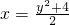∴函数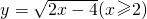的反函数是y=
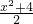（x≥0），
（2）任取0≤x1＜x2，则f（x2）-f（x1）=1-x22-1+x12
=x12-x22=（x1-x2）（x1+x2）
∵0≤x1＜x2，∴x1-x2＜0，x1+x2＞0
∴f（x2）-f（x1）＜0，即f（x2）＜f（x1）
故f（x）=1-x2在[0，+∞）上为单调减函数．
分析：（1）从条件中函数式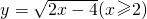中反解出x，再将x，y互换即得函数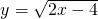（x≥2）的反函数．
（2）利用函数单调性的定义进行证明．任取1＜x1＜x2，我们构造出f（x2）-f（x1）的表达式，根据实数的性质，我们易出f（x2）-f（x1）的符号，进而根据函数单调性的定义，得到答案．注意化简f（x2）-f（x1）是一定要化到最简．
点评：本小题主要考查函数单调性的判断与证明、反函数的知识点，解答（1）题的关键是熟悉求反函数的一般步骤，注意反函数的定义域和值域的求解，本题比较基础．
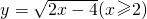，∴y2=2x-4，（y≥0），
∴
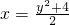，∴函数
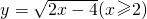的反函数是y=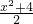（x≥0），（2）任取0≤x1＜x2，则f（x2）-f（x1）=1-x22-1+x12
=x12-x22=（x1-x2）（x1+x2）
∵0≤x1＜x2，∴x1-x2＜0，x1+x2＞0
∴f（x2）-f（x1）＜0，即f（x2）＜f（x1）
故f（x）=1-x2在[0，+∞）上为单调减函数．
分析：（1）从条件中函数式
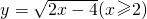中反解出x，再将x，y互换即得函数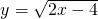（x≥2）的反函数．（2）利用函数单调性的定义进行证明．任取1＜x1＜x2，我们构造出f（x2）-f（x1）的表达式，根据实数的性质，我们易出f（x2）-f（x1）的符号，进而根据函数单调性的定义，得到答案．注意化简f（x2）-f（x1）是一定要化到最简．
点评：本小题主要考查函数单调性的判断与证明、反函数的知识点，解答（1）题的关键是熟悉求反函数的一般步骤，注意反函数的定义域和值域的求解，本题比较基础．
练习册系列答案
名校课堂系列答案
相关题目
例1、已知函数f(x)=
的定义域为A，函数y=f[f（x）]的定义域为B，则（ ）
| 1+x |
| 1-x |
| A、A∪B=B | B、A不属于B |
| C、A=B | D、A∩B=B |