题目内容
5.定义在R上的函数f(x)满足f(-x)+f(x)=0,f(x+2)=-f(x),且x∈(-2,0)时,f(x)=2x+$\frac{1}{5}$,则f(log220)=( )| A. | 1 | B. | $\frac{4}{5}$ | C. | -1 | D. | $-\frac{3}{5}$ |
分析 由已知中函数f(x)满足f(-x)+f(x)=0,f(x+2)=-f(x),log220∈(4,5),可得f(log220)=-f(4-log220),代入可得答案.
解答 解:∵函数f(x)满足f(-x)+f(x)=0,f(x+2)=-f(x),log220∈(4,5),
∴f(log220)=-f(log220-2)=f(log220-4)=-f(4-log220),
又∵x∈(-2,0)时,f(x)=2x+$\frac{1}{5}$,f(4-log220)=1,
∴f(log220)=-1,
故选:C
点评 本题考查的知识点焊 抽象函数及其应用,函数求值,难度中档.

练习册系列答案
相关题目
6.若无穷等差数列{an}的首项a1<0,公差d>0,{an}的前n项和为Sn,则以下结论中一定正确的是( )
| A. | Sn单调递增 | B. | Sn单调递减 | C. | Sn有最小值 | D. | Sn有最大值 |
16.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{5}$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
20.若方程x2+y2-4x+2y+5k=0表示圆,则k的取值范围是( )
| A. | k>1 | B. | k<1 | C. | k≥1 | D. | k≤1 |
17.某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如表关系:
(1)画出散点图,并判断y与x是否具有线性相关关系?
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)
15.定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则下列不等式一定成立的是( )
| A. | f( cos$\frac{2π}{3}$)>f(sin$\frac{2π}{3}$) | B. | f(sin 1)<f(cos 1) | ||
| C. | f(sin$\frac{π}{6}$)<f(cos$\frac{π}{6}$) | D. | f(cos 2)>f(sin 2) |
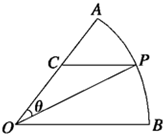 公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ;
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ; 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证: