题目内容
直线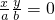 称为椭圆
称为椭圆 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率 .
.
(Ⅰ)求椭圆的“特征直线”方程;
(Ⅱ)过椭圆C上一点M(x0,y0)(x0≠0)作圆x2+y2=b2的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若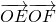 取值范围恰为
取值范围恰为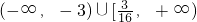 ,求椭圆C的方程.
,求椭圆C的方程.
解:(Ⅰ)设c2=a2-b2(c>0),则由 ,得
,得 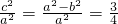 ,
,
∴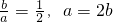 ,椭圆的“特征直线”方程为:x±2y=0.
,椭圆的“特征直线”方程为:x±2y=0.
(Ⅱ)根据P、Q是以MO为直径的圆和圆x2+y2=b2的交点,把两圆的方程相减可得
直线PQ的方程,并化为一般式为 x0x+y0y=b2,设E(x1,y1),F(x2,y2),
联立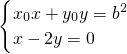 ,解得
,解得 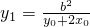 . 同理可求
. 同理可求 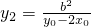 ,
,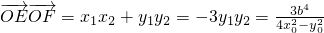 ,∵M(x0,y0)是椭圆上的点,
,∵M(x0,y0)是椭圆上的点,
∴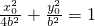 ,从而
,从而  ,
,
∵0<x02≤4b2 ,∴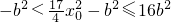 ,∴
,∴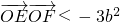 ,或
,或 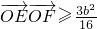 ,
,
由条件得 b2=1,故椭圆C的方程为 .
.
分析:(Ⅰ) 由离心率的值求得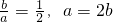 ,即得特征直线
,即得特征直线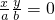 的方程.
的方程.
(Ⅱ) 用点斜式求出直线PQ的方程,与圆的方程联立求得E的纵坐标y1 ,同理求得F的纵坐标y2,再根据点M满足的条件及两个向量的数量积公式求得,由0<x02≤4b2 进一步化简得,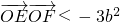 ,或
,或 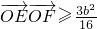 ,结合条件有 b2=1,从而得到 椭圆C的方程.
,结合条件有 b2=1,从而得到 椭圆C的方程.
点评:本题考查椭圆的简单性质,两个向量的数量积公式,以及不等式的性质的应用.
 ,得
,得 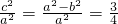 ,
,∴
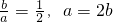 ,椭圆的“特征直线”方程为:x±2y=0.
,椭圆的“特征直线”方程为:x±2y=0.(Ⅱ)根据P、Q是以MO为直径的圆和圆x2+y2=b2的交点,把两圆的方程相减可得
直线PQ的方程,并化为一般式为 x0x+y0y=b2,设E(x1,y1),F(x2,y2),
联立
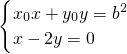 ,解得
,解得 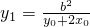 . 同理可求
. 同理可求 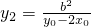 ,
,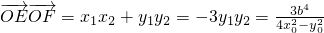 ,∵M(x0,y0)是椭圆上的点,
,∵M(x0,y0)是椭圆上的点,∴
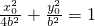 ,从而
,从而  ,
,∵0<x02≤4b2 ,∴
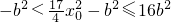 ,∴
,∴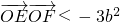 ,或
,或 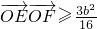 ,
,由条件得 b2=1,故椭圆C的方程为
 .
.分析:(Ⅰ) 由离心率的值求得
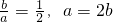 ,即得特征直线
,即得特征直线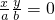 的方程.
的方程.(Ⅱ) 用点斜式求出直线PQ的方程,与圆的方程联立求得E的纵坐标y1 ,同理求得F的纵坐标y2,再根据点M满足的条件及两个向量的数量积公式求得,由0<x02≤4b2 进一步化简得,
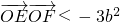 ,或
,或 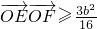 ,结合条件有 b2=1,从而得到 椭圆C的方程.
,结合条件有 b2=1,从而得到 椭圆C的方程.点评:本题考查椭圆的简单性质,两个向量的数量积公式,以及不等式的性质的应用.

练习册系列答案
相关题目
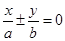 称为椭圆
称为椭圆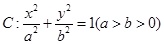 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率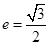 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;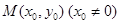 作圆
作圆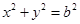 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若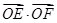 取值范围恰为
取值范围恰为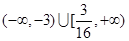 ,求椭圆C的方程.
,求椭圆C的方程.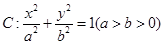 的焦点和上顶点分别为
的焦点和上顶点分别为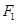 、
、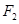 、
、 ,我们称
,我们称 为椭圆
为椭圆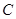 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.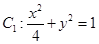 和
和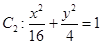 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出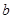 的椭圆为
的椭圆为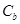 ,且直线
,且直线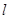 与椭圆为
与椭圆为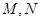 (异于端点),试问:当
(异于端点),试问:当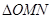 面积最大时,
面积最大时,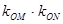 是否与
是否与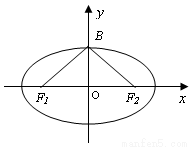
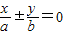 称为椭圆
称为椭圆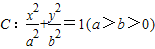 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率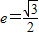 .
.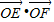 取值范围恰为
取值范围恰为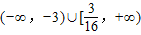 ,求椭圆C的方程.
,求椭圆C的方程. 称为椭圆
称为椭圆 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率 .
. 取值范围恰为
取值范围恰为 ,求椭圆C的方程.
,求椭圆C的方程.