题目内容
平面上有两个定点A,B,另有4个与A,B不重合的动点C1,C2,C3,C4。若使
 ,则称(
,则称( )为一个好点对.那
)为一个好点对.那
么这样的好点对( )
| A.不存在 | B.至多有一个 | C.至少有一个 | D.恰有一个 |
C
解析试题分析:因为,
 ,所以,
,所以, 。将区间[0,1]分成[0,
。将区间[0,1]分成[0,  ],[
],[ ,
, ],[
],[ ,1]三段,则C1,C2,C3,C4中至少有两个值落在同一个小区间内(抽屉原理)。所以满足的好点对
,1]三段,则C1,C2,C3,C4中至少有两个值落在同一个小区间内(抽屉原理)。所以满足的好点对 至少有一个。所以选C.
至少有一个。所以选C.
考点:三角函数的性质,“抽屉原理”。
点评:难题,本题源于2009年安徽数学竞赛试题,从思路的探寻方面,难度较大。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知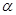 为第三象限角,则
为第三象限角,则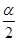 所在的象限是( )
所在的象限是( )
| A.第一或第二象限 | B.第二或第三象限 | C.第一或第三象限 | D.第二或第四象限角 |
已知函数 在
在 上单调递减,则
上单调递减,则 的取值范围
的取值范围
A. | B.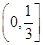 | C. | D. |
若函数 ,则
,则 是
是
A.最小正周期为 的奇函数 的奇函数 | B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为2 的偶函数 的偶函数 | D.最小正周期为 的偶函数 的偶函数 |
把函数 的图象按向量
的图象按向量 平移,得到函数
平移,得到函数 的图象,则
的图象,则 可以是:( )
可以是:( )
A.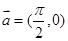 | B. | C. | D. |
若函数 
 在区间
在区间 上单调递增,则实数
上单调递增,则实数  的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
(5分)函数 的部分图象如图所示,则ω,φ的值分别是( )
的部分图象如图所示,则ω,φ的值分别是( )
A. | B. | C. | D. |
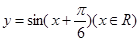 图像上所有的点向左平行移动
图像上所有的点向左平行移动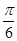 个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图像的解析式为( )
个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图像的解析式为( )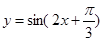
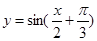
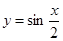
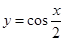
 个单位后,得到一个偶函数的图像,则φ的一个可能取值为( )
个单位后,得到一个偶函数的图像,则φ的一个可能取值为( )

