Question

已知函数在上单调递减，则的取值范围

A．

B．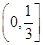

C．

D．

Answer 1

C  

解析试题分析：∵x∈，ω＞0，∴ωx+∈[+,+]
∵函数f(x)=sin(ωx+)在上单调递减，∴周期T=≥，解得ω≤4,
∵f(x)=sin(ωx+)的减区间满足：
+2kπ＜ωx+＜+2kπ，k∈Z,∴取k=0，得+,+，解之得
≤ω≤
故选C.
考点：正弦型函数的单调性
点评：中档题，对正弦型函数的研究，注意将看作一个整体。