题目内容

（2011•顺义区一模）已知数列{an}中，a1=
1
2
，a2=
3
4
，当n≥2时，有2an+1=3an-an-1，（n∈N*）成立．则a4=
15
16
15
16
．
分析：利用递推式，代入计算，即可得到结果．
解答：解：∵数列{an}中，a1=
1
2
，a2=
3
4
，2an+1=3an-an-1，
∴2a3=3a2-a1=
7
4

∴a3=
7
8

∴2a4=3a3-a2=
15
8

∴a4=
15
16

故答案为：
15
16
点评：本题考查数列递推式，解题的关键是代入计算，属于基础题．
练习册系列答案
相关题目
（2011•顺义区一模）已知全集U=R，集合M={x|-1≤x≤1}，N={x|x≥0}，M∩（CUN）=（　　）
（2011•顺义区一模）已知i为虚数单位，则i（2i+1）=（　　）
（2011•顺义区一模）下列函数中，既是偶函数，又在区间（0，+∞）上单调递减的函数为（　　）
（2011•顺义区一模）已知|
a
|=1，|
b
|=2，
a
•(
b
-
a
)=
3
-1，则
a
与
b
的夹角是（　　）
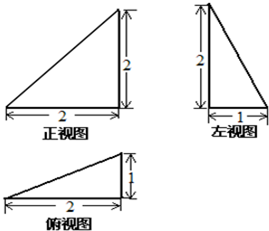（2011•顺义区一模）一个几何体的三视图如图所示，则其表面积等于（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网