题目内容
在△ABC中,“cosA•cosB•cosC<0”是“△ABC为钝角三角形”的( )
分析:根据三角形的几何特征,及余弦函数的符号,我们分别确定“cosA•cosB•cosC<0”⇒“△ABC为钝角三角形”与“△ABC为钝角三角形”⇒“cosA•cosB•cosC<0”的真假,进而根据充要条件的定义,即可得到答案.
解答:解:由于△ABC中,A,B,C只少存在两个锐角
故cosA,cosB,cosC中至少有两个正值
则“cosA•cosB•cosC<0”⇒“△ABC为钝角三角形”为真命题;
“△ABC为钝角三角形”⇒“cosA•cosB•cosC<0”为真命题;
故“cosA•cosB•cosC<0”是“△ABC为钝角三角形”的充要条件
故选A
故cosA,cosB,cosC中至少有两个正值
则“cosA•cosB•cosC<0”⇒“△ABC为钝角三角形”为真命题;
“△ABC为钝角三角形”⇒“cosA•cosB•cosC<0”为真命题;
故“cosA•cosB•cosC<0”是“△ABC为钝角三角形”的充要条件
故选A
点评:本题考查的知识点是充要条件的定义,余弦函数的符号,其中判断出“cosA•cosB•cosC<0”⇒“△ABC为钝角三角形”与“△ABC为钝角三角形”⇒“cosA•cosB•cosC<0”的真假,是解答本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
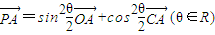 ,则
,则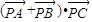 的最小值是 .
的最小值是 .