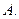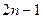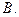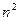题目内容
(本小题共12分)设数列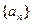 的前
的前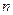 项和为
项和为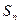 ,已知
,已知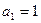 ,
,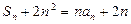 (
(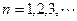 ).(Ⅰ)求证:数列
).(Ⅰ)求证:数列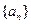 为等差数列,并分别写出
为等差数列,并分别写出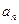 和
和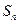 关于
关于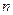 的表达式;(Ⅱ)若
的表达式;(Ⅱ)若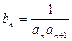 ,
,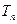 为数列
为数列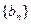 前
前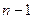 项和,求
项和,求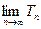 ;(Ⅲ)是否存在自然数
;(Ⅲ)是否存在自然数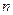 ,使得
,使得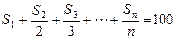 ? 若存在,求
? 若存在,求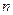 的值;若不存在,说明理由.
的值;若不存在,说明理由.
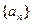 的前
的前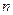 项和为
项和为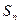 ,已知
,已知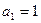 ,
,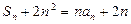 (
(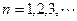 ).(Ⅰ)求证:数列
).(Ⅰ)求证:数列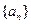 为等差数列,并分别写出
为等差数列,并分别写出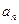 和
和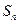 关于
关于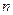 的表达式;(Ⅱ)若
的表达式;(Ⅱ)若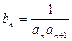 ,
,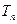 为数列
为数列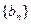 前
前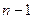 项和,求
项和,求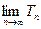 ;(Ⅲ)是否存在自然数
;(Ⅲ)是否存在自然数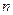 ,使得
,使得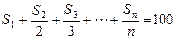 ? 若存在,求
? 若存在,求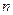 的值;若不存在,说明理由.
的值;若不存在,说明理由. (Ⅰ)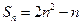 (Ⅱ)
(Ⅱ) 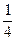 .(Ⅲ)
.(Ⅲ)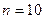
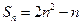 (Ⅱ)
(Ⅱ) 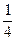 .(Ⅲ)
.(Ⅲ)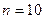
:(Ⅰ)当 时,
时,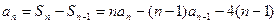 ,
,
得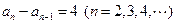 . ∴数列
. ∴数列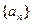 是以
是以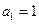 为首项,4为公差的等差数列.
为首项,4为公差的等差数列.
∴
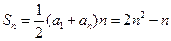 .
.
(Ⅱ)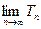 =
=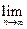
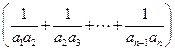
=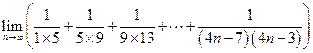
=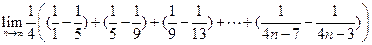 =
=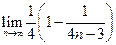 =
=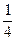 .
.
(Ⅲ)由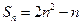 得:
得: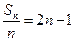 ,
,
∴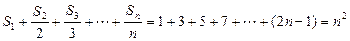 .
.
令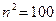 ,得
,得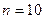 ,所以,存在满足条件的自然数
,所以,存在满足条件的自然数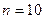 .
.
 时,
时,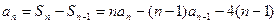 ,
,得
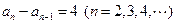 . ∴数列
. ∴数列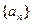 是以
是以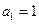 为首项,4为公差的等差数列.
为首项,4为公差的等差数列. ∴

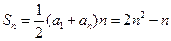 .
. (Ⅱ)
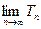 =
=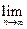
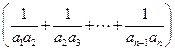
=
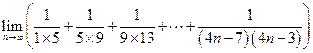
=
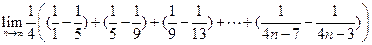 =
=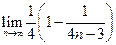 =
=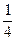 .
. (Ⅲ)由
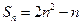 得:
得: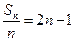 ,
,∴
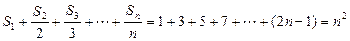 .
. 令
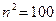 ,得
,得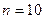 ,所以,存在满足条件的自然数
,所以,存在满足条件的自然数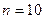 .
. 
练习册系列答案
相关题目
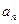 的信息如下图。
的信息如下图。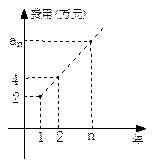
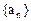 满足
满足
 ,则
,则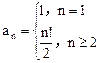
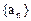 满足
满足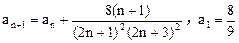 ,求数列
,求数列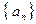 的前
的前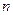 项和为
项和为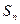 ,
,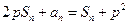
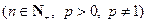 ,数列
,数列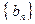 满足
满足 .(Ⅰ)求数列
.(Ⅰ)求数列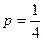 时,
时,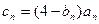 ,求数列
,求数列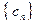 的前
的前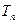 .
.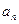 }中的相邻两项
}中的相邻两项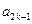 、
、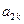 是关于x的方程
是关于x的方程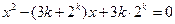 的两个根,且
的两个根,且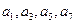 及
及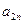 (n≥4)(不必证明);
(n≥4)(不必证明);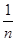 ),f(
),f(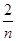 ),
),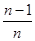 )……,(n≥2,n∈
)……,(n≥2,n∈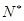 )的前n项的和为Sn ;
)的前n项的和为Sn ;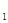 =
=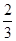 ,a
,a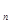 =" "
=" " 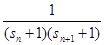 (n≥2,n∈
(n≥2,n∈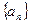 的公差为2,若
的公差为2,若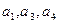 成等比数列, 则
成等比数列, 则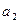 =" ( " )
=" ( " )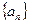 中,
中,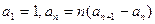 ,则数列
,则数列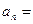 ( )
( )