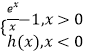МвДҝДЪИЭ
ЎҫМвДҝЎҝұұҫ©Кұјд3ФВ15ИХПВОзЈ¬№ИёиО§ЖеИЛ№ӨЦЗДЬ ![]() Улә«№ъЖеКЦАоКАКҜҪшРРЧоәуТ»ВЦҪПБҝЈ¬
Улә«№ъЖеКЦАоКАКҜҪшРРЧоәуТ»ВЦҪПБҝЈ¬ ![]() »сөГұҫіЎұИИьКӨАыЈ¬ЧоЦХИЛ»ъҙуХҪЧЬұИ·Ц¶Ёёс
»сөГұҫіЎұИИьКӨАыЈ¬ЧоЦХИЛ»ъҙуХҪЧЬұИ·Ц¶Ёёс ![]() .ИЛ»ъҙуХҪТІТэ·ўИ«Гс¶ФО§ЖеөД№ШЧўЈ¬ДіС§РЈЙзНЕОӘөчІйС§ЙъС§П°О§ЖеөДЗйҝцЈ¬Лж»ъійИЎБЛ100ГыС§ЙъҪшРРөчІй.ёщҫЭөчІйҪб№ы»жЦЖөДС§ЙъИХҫщС§П°О§ЖеКұјдөДЖөВК·ЦІјЦұ·ҪНјЈЁИзНјЛщКҫЈ©Ј¬Ҫ«ИХҫщС§П°О§ЖеКұјдІ»өНУЪ40·ЦЦУөДС§ЙъіЖОӘЎ°О§ЖеГФЎұ.
.ИЛ»ъҙуХҪТІТэ·ўИ«Гс¶ФО§ЖеөД№ШЧўЈ¬ДіС§РЈЙзНЕОӘөчІйС§ЙъС§П°О§ЖеөДЗйҝцЈ¬Лж»ъійИЎБЛ100ГыС§ЙъҪшРРөчІй.ёщҫЭөчІйҪб№ы»жЦЖөДС§ЙъИХҫщС§П°О§ЖеКұјдөДЖөВК·ЦІјЦұ·ҪНјЈЁИзНјЛщКҫЈ©Ј¬Ҫ«ИХҫщС§П°О§ЖеКұјдІ»өНУЪ40·ЦЦУөДС§ЙъіЖОӘЎ°О§ЖеГФЎұ.
ЈЁўсЈ©ёщҫЭТСЦӘМхјюНкіЙПВГжөДБРБӘұнЈ¬ІўҫЭҙЛЧКБПДгКЗ·сУР ![]() өД°СОХИПОӘЎ°О§ЖеГФЎұУлРФұрУР№ШЈҝ
өД°СОХИПОӘЎ°О§ЖеГФЎұУлРФұрУР№ШЈҝ
·ЗО§ЖеГФ | О§ЖеГФ | әПјЖ | |
ДР | |||
Е® | 10 | 55 | |
әПјЖ |
ЈЁўтЈ©Ҫ«ЙПКцөчІйЛщөГөҪөДЖөВККУОӘёЕВКЈ¬ПЦФЪҙУёГөШЗшҙуБҝС§ЙъЦРЈ¬ІЙУГЛж»ъійСщ·Ҫ·ЁГҝҙОійИЎ1ГыС§ЙъЈ¬ійИЎ3ҙОЈ¬јЗұ»ійИЎөД3Гыөӯ¶ЁЙъЦРөДЎ°О§ЖеГФЎұИЛКэОӘ ![]() ЎЈИфГҝҙОійИЎөДҪб№ыКЗПа»Ҙ¶АБўөДЈ¬Зу
ЎЈИфГҝҙОійИЎөДҪб№ыКЗПа»Ҙ¶АБўөДЈ¬Зу ![]() өД·ЦІјБРЈ¬ЖЪНы
өД·ЦІјБРЈ¬ЖЪНы ![]() әН·ҪІо
әН·ҪІо ![]() .
.
ёҪЈә ![]() Ј¬ЖдЦР
Ј¬ЖдЦР ![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
Ўҫҙр°ёЎҝҪвЈәЈЁўсЈ©УЙЖөВК·ЦІјЦұ·ҪНјҝЙЦӘЈ¬ФЪійИЎөД100ИЛЦРЈ¬Ў°О§ЖеГФЎұУР25ИЛЈ¬ҙУ¶ш ![]() БРБӘұнИзПВ
БРБӘұнИзПВ
·ЗО§ЖеГФ | О§ЖеГФ | әПјЖ | |
ДР | 30 | 15 | 45 |
Е® | 45 | 10 | 55 |
әПјЖ | 75 | 25 | 100 |
Ҫ« ![]() БРБӘұнЦРөДКэҫЭҙъИ빫КҪјЖЛгЈ¬өГ
БРБӘұнЦРөДКэҫЭҙъИ빫КҪјЖЛгЈ¬өГ![]()
ТтОӘ ![]() Ј¬ЛщТФГ»УРАнУЙИПОӘЎ°О§ЖеГФЎұУлРФұрУР№Ш.
Ј¬ЛщТФГ»УРАнУЙИПОӘЎ°О§ЖеГФЎұУлРФұрУР№Ш.
ЈЁўтЈ©УЙЖөВК·ЦІјЦұ·ҪНјЦӘійөҪЎ°О§ЖеГФЎұөДЖөВКОӘ0.25Ј¬Ҫ«ЖөВККУОӘёЕВКЈ¬јҙҙУ№ЫЦЪЦРійИЎТ»ГыЎ°О§ЖеГФЎұөДёЕВКОӘ ![]() .УЙМвТв
.УЙМвТв ![]() Ј¬ҙУ¶ш
Ј¬ҙУ¶ш ![]() өД·ЦІјБРОӘ
өД·ЦІјБРОӘ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
. ![]() .
.
ЎҫҪвОцЎҝұҫМвЦчТӘҝјІйБЛЖөВК·ЦІјЦұ·ҪНјЈ¬ТФј°¶АБўјмСйКэС§ЖЪНыөДЗу·ЁөДУҰУГЎЈЈЁ1Ј©ёщҫЭЖөВК·ЦІјЦұ·ҪНјМоРҙ2ЎБ2·ЦІјНјЈ¬јЖЛг№ЫІвЦөЈ¬ұИҪПБЩҪзЦөјҙҝЙөГҪбВЫЎЈЈЁ2Ј©УЙЖөВК·ЦІјЦұ·ҪНјјЖЛгЖөВКЈ¬Ҫ«ЖөВККУОӘёЕВКЈ¬И»әуУЙ·ЦІјБРЈ¬ёщҫЭКэС§ЖЪНыјЖЛгЗуҪвЎЈ
Ўҫҝјөгҫ«ОцЎҝИПХжЙуМвЈ¬КЧПИРиТӘБЛҪвЖөВК·ЦІјЦұ·ҪНј(ЖөВК·ЦІјұнәНВК·ЦІјЦұ·ҪНјЈ¬КЗ¶ФПаН¬КэҫЭөДБҪЦЦІ»Н¬ұнҙп·ҪКҪ.УГҪфҙХөДұнёсёДұдКэҫЭөДЕЕБР·ҪКҪәН№№іЙРОКҪЈ¬ҝЙХ№КҫКэҫЭөД·ЦІјЗйҝц.НЁ№эЧчНјјИҝЙТФҙУКэҫЭЦРМбИЎРЕПўЈ¬УЦҝЙТФАыУГНјРОҙ«өЭРЕПў)Ј®

 53ЛжМГІвПөБРҙр°ё
53ЛжМГІвПөБРҙр°ё