题目内容
用一个平面截一个长方体，截出的截面是一个三角形，则这个三角形的形状是（ ）
分析：由于截出的截面是一个三角形，用余弦定理判断截面各角的大小，可判断这个三角形的形状．
解答：解：如图，在图中的长方体，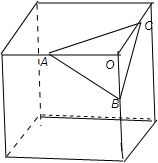
如一个平面α截此正方体，截面是三角形ABC，
设OA=a，OB=b，OC=c，AC2=a2+c2，AB2=a2+b2，BC2=b2+c2，
∴cos∠CAB=
＞0，
∴∠CAB为锐角，
同理∠ACB与∠ABC也为锐角，
所以△ABC为锐角三角形，
故选A．
如一个平面α截此正方体，截面是三角形ABC，设OA=a，OB=b，OC=c，AC2=a2+c2，AB2=a2+b2，BC2=b2+c2，
∴cos∠CAB=
| 2a2 | ||||
2(a2+c2)
|
∴∠CAB为锐角，
同理∠ACB与∠ABC也为锐角，
所以△ABC为锐角三角形，
故选A．
点评：本题考查了正方体的几何特征，熟练掌握正方体模型中包含的线面长度及位置关系是解答的关键．
练习册系列答案
相关题目