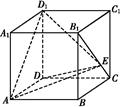
题目内容
如图, 为圆
为圆 的直径,点
的直径,点 .
. 在圆
在圆 上,且
上,且 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, .
.

(1)设 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
 为圆
为圆 的直径,点
的直径,点 .
. 在圆
在圆 上,且
上,且 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, .
.
(1)设
 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;(2)求四棱锥
 的体积.
的体积.(1)证明详见解析;(2)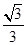 .
.
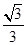 .
.试题分析:(1)要证
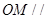 平面
平面 ,根据直线与平面平行的判定定理可知只需证
,根据直线与平面平行的判定定理可知只需证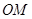 与平面
与平面 内一直线平行即可,设
内一直线平行即可,设 的中点为
的中点为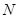 ,则
,则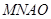 为平行四边形,则
为平行四边形,则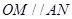 ,又
,又 平面
平面 ,
,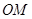 不在平面
不在平面 内,满足定理所需条件;(2)过点
内,满足定理所需条件;(2)过点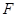 作
作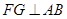 于
于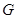 ,根据面面垂直的性质可知
,根据面面垂直的性质可知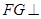 平面
平面 ,
,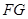 即正
即正 的高,然后根据三棱锥的体积公式进行求解即可.
的高,然后根据三棱锥的体积公式进行求解即可.试题解析:(1)设
 的中点为
的中点为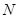 ,则
,则
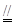


又

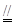
 ,∴
,∴
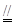

∴
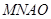 为平行四边形∴
为平行四边形∴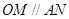
又
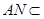 平面
平面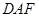 ,
,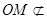 平面
平面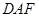
∴
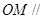 平面
平面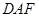
(2)过点
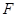 作
作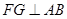 于
于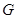
 平面
平面 平面
平面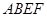 ,∴
,∴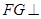 平面
平面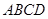 ,
,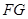 即正
即正 的高
的高∴
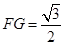 ∴
∴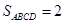
∴
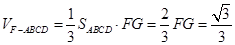 .
.
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
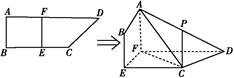
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
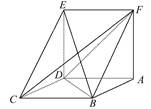
 ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.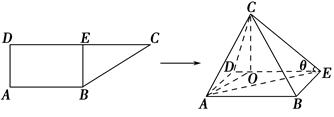
 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为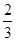 ,则这个球的表面积为( )
,则这个球的表面积为( )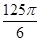
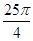
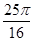

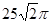

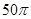
 A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A
A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A