题目内容
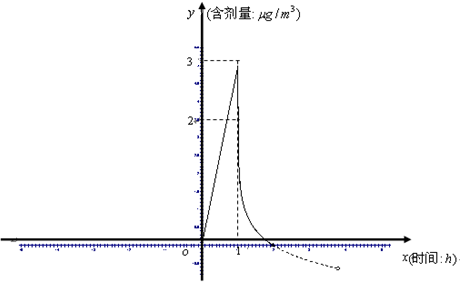
某种空气清洁剂在实验效果时,发现空气含剂量y(μg/m3)与时间x之间存在函数关系,其变化的图象如下图所示.其中的曲线部分是某函数y=log
(x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.
(1)求出空气含剂量y关于时间x的函数表达式及定义域.
(2)实验证明,当空气含剂量不低于2μg/m3时,空气清洁的效果最佳.求一次喷洒的“最佳效果”持续时间.
| 1 |
| 2 |
(1)求出空气含剂量y关于时间x的函数表达式及定义域.
(2)实验证明,当空气含剂量不低于2μg/m3时,空气清洁的效果最佳.求一次喷洒的“最佳效果”持续时间.

(1)当x≤1时,图象是一线段,得解析式为y=kx,将点(1,3)坐标代入得k=3,∴y=3x
把(1,3)坐标代入y=log
(x+b)得.
=3,∴1+b=(
)3=
,∴b=-
∴y=
∴,令y=0得x=
∴函数的解析式为:y=
(2)当0≤x≤1时,在y=3x中令y=2得x1=
,
当1≤x≤
时,在y=
中,令y=2得:
=2,得x2=
x=x2-x1=
-
=
故最佳效果持续时间为
小时.
把(1,3)坐标代入y=log
| 1 |
| 2 |
| log | (1+b)
|
| 1 |
| 2 |
| 1 |
| 8 |
| 7 |
| 8 |
| log | (x-
|
∴,令y=0得x=
| 15 |
| 8 |
∴函数的解析式为:y=
|
(2)当0≤x≤1时,在y=3x中令y=2得x1=
| 2 |
| 3 |
当1≤x≤
| 15 |
| 8 |
| log | (x-
|
中,令y=2得:
| log | (x-
|
| 9 |
| 8 |
x=x2-x1=
| 9 |
| 8 |
| 2 |
| 3 |
| 11 |
| 24 |
故最佳效果持续时间为
| 11 |
| 24 |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

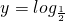 (x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.
(x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.
 (x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.
(x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.