题目内容
设抛物线y=
的焦点为F，准线为l，过点F的直线斜率为k，且与抛物线交于A；B两点，P在准线l上.(Ⅰ)当k=1且直线PA与PB相互垂直时，求点P的坐标；
(Ⅱ)设P(k，
)，试问是否存在常数λ；使等式
恒成立?若存在，求出λ的值；若不存在，说明理由.
答案：(I)∵x2=2y,∴焦点F(0,)；准线方程为：y=-.
又∵k=1,∴过F的直线：y=x+;设A(x1,x1+
),B(x2,x2+
);
由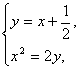
已知：x2-2x-1=0.∴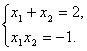
设P(x,y),∵P在准线上,故y=-
.
∴
∴
∴
∴x2-2x+1=0∴x=1∴P(1,-
).(6分)
(Ⅱ)
∴
∴
练习册系列答案
孟建平名校考卷系列答案
相关题目
＝(
，0)平移后，得到抛物线C，若C与直线L：x＋y＋m＝0(m≥0)交于A、B不同两点，设抛物线C的焦点为F，(1)试求u＝m
的值(用m表)(2)当u取最大值时，试求L的方程．
=4x，O为坐标原点，P为抛物线的准线与其对称轴的交点，过焦点F且垂直于x轴的直线交抛物线于M、N两点，若直线PM与ON相交于点Q，则cos∠MQN=
B．－
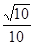D．－