题目内容
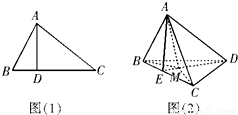 如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
【答案】分析:利用类比推理,将平面中的线与空间中的面类比,得到类比结论.
通过连接DM,据BC⊥AM,BC⊥AD得到BC⊥ADE得到BC⊥ED得到满足平面条件的三角形AED,利用平面三角形的性质得证.
解答:解:命题是:三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,
则有S△ABC2=S△BCM•S△BCD是一个真命题.
证明如下:
在图(2)中,连接DM,并延长交BC于E,连接AE,则有DE⊥BC.
因为AD⊥面ABC,所以AD⊥AE.
又AM⊥DE,所以AE2=EM•ED.
于是
 =S△BCM•S△BCD.
=S△BCM•S△BCD.
故有S△ABC2=S△BCM•S△BCD
点评:本题考查类比推理及利用平面的性质证明空间的结论.考查空间想象能力,逻辑思维能力.
通过连接DM,据BC⊥AM,BC⊥AD得到BC⊥ADE得到BC⊥ED得到满足平面条件的三角形AED,利用平面三角形的性质得证.
解答:解:命题是:三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,
则有S△ABC2=S△BCM•S△BCD是一个真命题.
证明如下:
在图(2)中,连接DM,并延长交BC于E,连接AE,则有DE⊥BC.
因为AD⊥面ABC,所以AD⊥AE.
又AM⊥DE,所以AE2=EM•ED.
于是

 =S△BCM•S△BCD.
=S△BCM•S△BCD.故有S△ABC2=S△BCM•S△BCD
点评:本题考查类比推理及利用平面的性质证明空间的结论.考查空间想象能力,逻辑思维能力.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.

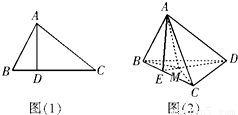 如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.