题目内容
F1、F2是椭圆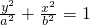
（a＞b＞0）的左、右焦点，B是该椭圆短轴的一个端点，直线BF1与椭圆C交于点A，若|AB|，|F1F2|，|AF2|成等差数列，则该椭圆的离心率为
- A.
- B.
- C.
- D.
A
分析：利用椭圆定义和|AB|，|F1F2|，|AF2|成成等差数列，及|AB|=|AF1|+|BF1|可得a，c之间的关系，可求离心率
解答：∵|AB|，|F1F2|，|AF2|成等差数列，
∴2|F1F2|=|AB|+|AF2|=|AF1|+|BF1|+|AF2|
由椭圆的定义可知，|AF1|+|AF2|=2a，|BF1|=a
∴4c=2a+a=3a
∴
=
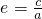故选A
点评：本题考查了等差数列的性质以及椭圆的简单性质，由椭圆定义和|AB|，|F1F2|，|AF2|成等差数列，能够得出啊，c之间的关系是解题的关键，属于中档题．
分析：利用椭圆定义和|AB|，|F1F2|，|AF2|成成等差数列，及|AB|=|AF1|+|BF1|可得a，c之间的关系，可求离心率
解答：∵|AB|，|F1F2|，|AF2|成等差数列，
∴2|F1F2|=|AB|+|AF2|=|AF1|+|BF1|+|AF2|
由椭圆的定义可知，|AF1|+|AF2|=2a，|BF1|=a
∴4c=2a+a=3a
∴
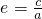=故选A
点评：本题考查了等差数列的性质以及椭圆的简单性质，由椭圆定义和|AB|，|F1F2|，|AF2|成等差数列，能够得出啊，c之间的关系是解题的关键，属于中档题．
练习册系列答案
相关题目
=1(a＞b＞0)的两个焦点，过F2作椭圆的弦AB，若△AF1B的周长为16，椭圆的离心率为e=
,求此椭圆方程.
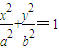（a＞b＞0）的左右焦点，A为上顶点，椭圆上的点N满足：
=
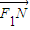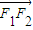+λ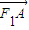
（λ∈R）．
，过点N作椭圆的切线分别交左、右准线于P、Q，直线NF1、NF2分别交椭圆于C、D两点．是否存在实数m，使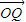
=m（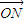
+
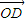）？若存在，求出实数m的值，否则说明理由；
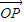=n（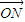
+
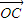）？若存在写出n的值．
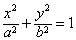（a>b>0）的左、右焦点，A是椭圆上位于第一象限内的一点，
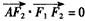，若椭圆的离心率等于
。
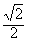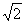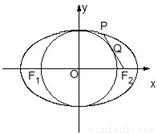
，求椭圆的方程。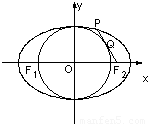 
如图，已知F1，F2是椭圆
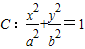（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为（ ）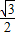
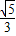
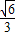
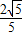
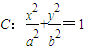（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则
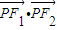= ；椭圆C的离心率为 ．