题目内容
已知公差不为0的等差数列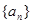 的首项
的首项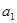 为a
为a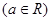 ,设数列的前n项和为
,设数列的前n项和为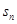 ,且
,且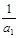 ,
,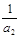 ,
,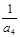 成等比数列.
成等比数列.
(1)求数列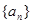 的通项公式及
的通项公式及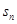 ;
;
(2)记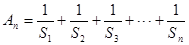 ,
,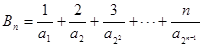 ,当
,当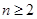 时,计算
时,计算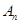 与
与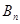 ,并比较
,并比较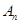 与
与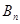 的大小(比较大小只需写出结果,不用证明).
的大小(比较大小只需写出结果,不用证明).
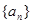 的首项
的首项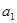 为a
为a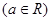 ,设数列的前n项和为
,设数列的前n项和为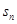 ,且
,且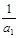 ,
,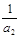 ,
,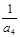 成等比数列.
成等比数列.(1)求数列
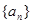 的通项公式及
的通项公式及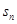 ;
;(2)记
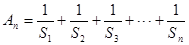 ,
,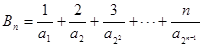 ,当
,当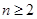 时,计算
时,计算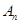 与
与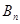 ,并比较
,并比较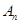 与
与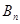 的大小(比较大小只需写出结果,不用证明).
的大小(比较大小只需写出结果,不用证明).(1)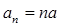 ,
,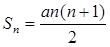 (2)
(2)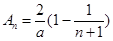 ,
,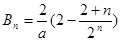
当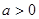 时,
时,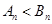 ;当
;当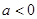 时,
时,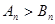
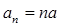 ,
,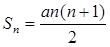 (2)
(2)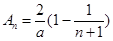 ,
,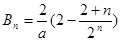
当
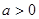 时,
时,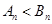 ;当
;当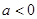 时,
时,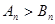
试题分析:(I)解:设等差数列
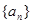 的公差为d,由
的公差为d,由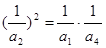 ,
,得
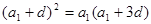 ,
,因为
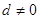 ,所以
,所以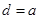 ,故
,故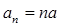 ,
,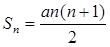 . 4分
. 4分(II)解:因为
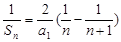 ,所以
,所以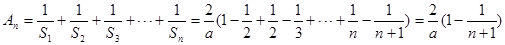 7分
7分∵
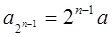 ,
,∴
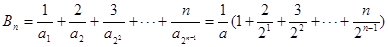 ,①
,①∴
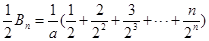 ,②
,②等式①②左右分别相减,得
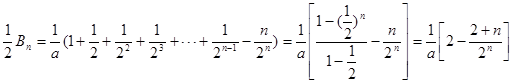
∴
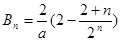 12分
12分当
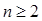 时,
时,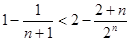 ,
,所以,当
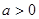 时,
时,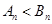 ;
;当
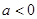 时,
时,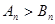 ? 14分
? 14分点评:第二问数列求和时用到了裂项相消和错位相减求和法,这两种方法是数列求和题目中常用的方法。裂项相消法一般适用于通项为
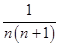 的形式,错位相减法一般适用于通项为
的形式,错位相减法一般适用于通项为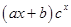 的形式的数列
的形式的数列
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.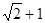 与
与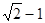 的等比中项等于 .
的等比中项等于 .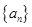 为等比数列,
为等比数列,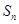 是它的前
是它的前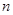 项和.若
项和.若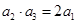 ,且
,且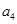 与
与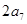 的等差中项为
的等差中项为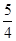 ,则
,则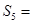
 中,
中, ,则
,则 ( )
( )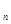 }的前三项和为13,首项为1,则其公比为
}的前三项和为13,首项为1,则其公比为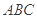 的内角
的内角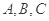 的对边分别为
的对边分别为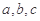 ,且
,且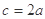 ,则
,则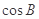 的值为
的值为
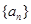 中
中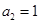 ,则其前3项的和
,则其前3项的和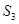 的取值范围是 ( )
的取值范围是 ( )