题目内容
16.在菱形ABCD中,若AC=4,则$\overrightarrow{CA}$•$\overrightarrow{AB}$等于( )| A. | 8 | B. | -8 | ||
| C. | |${\overrightarrow{AB}}$|cosA | D. | 与菱形的边长有关 |
分析 可画出图形,并设AC交BD于O点,从而便可得出OA⊥OB,且$\overrightarrow{CA}=2\overrightarrow{OA}$,$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,$|\overrightarrow{OA}|=2$,带入$\overrightarrow{CA}•\overrightarrow{AB}$进行向量数量积的运算即可得出$\overrightarrow{CA}•\overrightarrow{AB}$的值.
解答 解:如图,设AC∩BD=O,则OA⊥OB,且$\overrightarrow{CA}=2\overrightarrow{OA}$,$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,$|\overrightarrow{OA}|=2$;
∴$\overrightarrow{CA}•\overrightarrow{AB}=2\overrightarrow{OA}•(\overrightarrow{OB}-\overrightarrow{OA})$
=$2\overrightarrow{OA}•\overrightarrow{OB}-2{\overrightarrow{OA}}^{2}$
=0-8
=-8.
故选:B.
点评 考查菱形对角线的特点,向量减法和数乘的几何意义,以及向量数量积的运算.

练习册系列答案
相关题目
7.正实数x、y满足2x•2y=4,则实数xy的最大值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.根据气象记录,知道甲、乙两地一年中雨天占的比例分别为20%和18%,两地同时下雨的比例为12%,则甲地为雨天时乙地也为雨天的概率为( )
| A. | 0.12 | B. | 0.60 | C. | 0.67 | D. | 0.90 |
11.下列命题中正确的是( )
| A. | a>b,c>d⇒a-c>b-d | B. | ac2>bc2⇒a>b | C. | ac<bc⇒a<b | D. | a>b⇒$\frac{a}{c}$>$\frac{b}{c}$ |
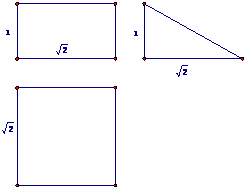 若某空间几何体的三视图如图所示.
若某空间几何体的三视图如图所示.