题目内容
已知函数f（x）=x2+ax+b，且对任意实数x都有f（x）=f（-m-x），其中m∈（0，2），那么
- A.f（-2）＜f（0）＜f（2）
- B.f（0）＜f（-2）＜f（2）
- C.f（0）＜f（2）＜f（-2）
- D.f（2）＜f（0）＜f（-2）
B
分析：通过用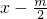
代换x，把f（x）=f（-m-x）化为
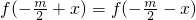，得f（x）的对称轴，求的 
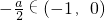，结合f（x）的图象，判出结论．
解答：对任意实数x都有f（x）=f（-m-x）
用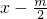代换x得：，
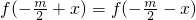所以函数f（x）=x2+ax+b的对称轴为：
，
而f（x）的对称轴为：
，
所以：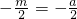
，即m=a，
因为a∈（0，2），所以，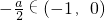
f（x）函数图象如图：
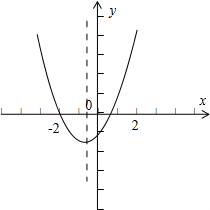
由图象的f（0）＜f（-2）＜f（2）．
故选B．
点评：本题考查比较函数值大小．用到了由抽象恒等式得出函数对称轴，以及二次函数图象的特征，再由图象特征作出判断．
分析：通过用
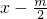代换x，把f（x）=f（-m-x）化为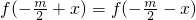，得f（x）的对称轴，求的 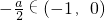，结合f（x）的图象，判出结论．解答：对任意实数x都有f（x）=f（-m-x）
用
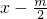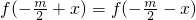代换x得：，所以函数f（x）=x2+ax+b的对称轴为：
，而f（x）的对称轴为：
，所以：
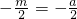，即m=a，因为a∈（0，2），所以
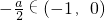，f（x）函数图象如图：
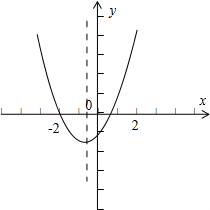
由图象的f（0）＜f（-2）＜f（2）．
故选B．
点评：本题考查比较函数值大小．用到了由抽象恒等式得出函数对称轴，以及二次函数图象的特征，再由图象特征作出判断．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|