题目内容
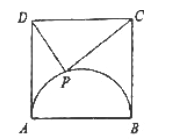
【题目】如图，
是边长为4的正方形，动点
在以
为直径的圆弧
上，则
的取值范围是__________．
【答案】
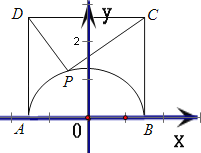
【解析】以AB中点为坐标原点，AB所在直线为x轴建立如图坐标系
则圆弧APB方程为x2+y2=4，（y≥0），C（2，4），D（﹣2，4）
因此设P（2cosα，2sinα），α∈[0，π]
∴
=（2﹣2cosα，4﹣2sinα），
=（﹣2﹣2cosα，4﹣2sinα），
由此可得
=（2﹣2cosα）（﹣2﹣2cosα）+（4﹣2sinα）（4﹣2sinα）
=4cos2α﹣4+16﹣16sinα+4sin2α=16﹣16sinα
化简得=16﹣16sinα
∵α∈[0，π]，sinα∈[0，1]
∴当α=0或π时，取最大值为16；当α=
时，取最小值为0．
由此可得的取值范围是[0，16]
故答案为：[0，16]
练习册系列答案
名校课堂系列答案
相关题目
