题目内容
17.在矩形ABCD中,AB=6,AD=4,点P在边AB上,点Q在AD上,△CPQ的面积为8,则∠PCQ的最大值是30°.分析 设∠BCP=α,∠DCQ=β,则CP=$\frac{4}{cos}$,CQ=$\frac{6}{cosβ}$,由此能推导出2sin∠PCQ=cos(α-β),从而能求出∠PCQ的最大值是30°.
解答 解:设∠BCP=α,∠DCQ=β,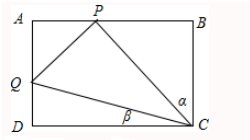
则CP=$\frac{4}{cos}$,CQ=$\frac{6}{cosβ}$,
∴${S}_{△CPQ}=\frac{1}{2}•\frac{4}{cosα}•\frac{6}{cosβ}•sin∠PCQ$=8,
∴3sin∠PCQ=2cosαcosβ,
∴3sin∠PCQ=cos(α+β)+cos(α-β),
∴$3sin∠PCQ=cos(\frac{π}{2}-∠PCD)$+cos(α-β),
∴2sin∠PCQ=cos(α-β),
∴sin∠PCQ=$\frac{1}{2}cos(α-β)≤\frac{1}{2}$,
当α=β时,等号成立,
∴∠PCQ≤30°,
∴则∠PCQ的最大值是30°.
故答案为:30°.
点评 本题考查角的最大值的求法,是中档题,解题时要认真审题,注意三角函数知识的灵活运用.

练习册系列答案
相关题目
7. 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )| A. | 1 | B. | -1 | C. | 2 | D. | ln4 |
19.已知随机变量ξ的分布列为ξ=-1,0,1,对应P=$\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$,且设η=2ξ+1,则η的期望为( )
| A. | -$\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{29}{36}$ | D. | 1 |
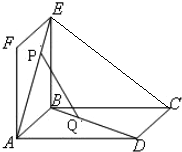 如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.