题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立;
恒成立;
(3)若正实数![]() 满足
满足![]() ,证明
,证明![]() .
.
【答案】(1)单调减区间为![]() ,函数
,函数![]() 的增区间是
的增区间是![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)求导函数,从而可确定函数的单调性;(2)构造函数![]() ,利用导数研究其最值,将恒成立问题进行转化;(3)将代数式
,利用导数研究其最值,将恒成立问题进行转化;(3)将代数式![]() 放缩,构造关于
放缩,构造关于![]() 的一元二次不等式,解不等式即可.
的一元二次不等式,解不等式即可.
试题解析:(1)![]() ,由
,由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() 的单调减区间为
的单调减区间为![]() ,函数
,函数![]() 的增区间是
的增区间是![]() ,
,
(2)令![]() ,
,
所以![]()
因为![]() ,
,
所以 ,令
,令![]() ,得
,得![]() ,
,
所以当![]() ;当
;当![]() 时,
时,![]() ,
,
因此函数![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数,
是减函数,
故函数![]() 的最大值为
的最大值为![]()
令![]() ,因为
,因为![]() ,又因为
,又因为![]() 在
在![]() 是减函数,
是减函数,
所以当![]() 时,
时,![]() ,即对于任意正数
,即对于任意正数![]() 总有
总有![]() ,
,
所以关于![]() 的不等式
的不等式![]() 恒成立;
恒成立;
(3)由![]() ,
,
即![]() ,
,
从而![]()
令![]() ,则由
,则由![]() 得,
得,![]() ,
,
可知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,又
,又![]() ,
,
因此![]() 成立.
成立.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中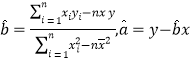 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).

