题目内容
函数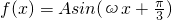 (其中A>0,ω>0)的振幅为2,周期为π.
(其中A>0,ω>0)的振幅为2,周期为π.
(1)求f(x)的解析式;
(2)求f(x)的单调增区间;
(3)求f(x)在 的值域.
的值域.
解:(1)∵函数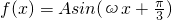 (其中A>0,ω>0)的振幅为2,周期为π.
(其中A>0,ω>0)的振幅为2,周期为π.
∴A=2,π= .解得ω=2.
.解得ω=2.
∴ .
.
(2)由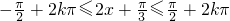 ,解得
,解得 (k∈Z).
(k∈Z).
∴f(x)的单调增区间为 ;
;
(3)∵ ,∴
,∴ .
.
∴f(x)的单调递减区间为 ;单调递增区间为
;单调递增区间为 .
.
∴当 时,即
时,即 时,函数f(x)取得最小值-2;
时,函数f(x)取得最小值-2;
当x=0时, 时,函数f(x)取得最大值
时,函数f(x)取得最大值 =
= .
.
故函数f(x)的值域为 .
.
分析:(1)利用振幅的定义和周期公式 ,即可得出;
,即可得出;
(2)利用正弦函数的单调性即可得出;
(3)由 ,可得
,可得 .进而得到f(x)的单调递减区间为
.进而得到f(x)的单调递减区间为 ;单调递增区间为
;单调递增区间为 .即可得到值域.
.即可得到值域.
点评:熟练掌握三角函数的图象与性质是解题的关键.
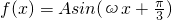 (其中A>0,ω>0)的振幅为2,周期为π.
(其中A>0,ω>0)的振幅为2,周期为π.∴A=2,π=
 .解得ω=2.
.解得ω=2.∴
 .
.(2)由
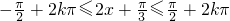 ,解得
,解得 (k∈Z).
(k∈Z).∴f(x)的单调增区间为
 ;
;(3)∵
 ,∴
,∴ .
.∴f(x)的单调递减区间为
 ;单调递增区间为
;单调递增区间为 .
.∴当
 时,即
时,即 时,函数f(x)取得最小值-2;
时,函数f(x)取得最小值-2;当x=0时,
 时,函数f(x)取得最大值
时,函数f(x)取得最大值 =
= .
.故函数f(x)的值域为
 .
.分析:(1)利用振幅的定义和周期公式
 ,即可得出;
,即可得出;(2)利用正弦函数的单调性即可得出;
(3)由
 ,可得
,可得 .进而得到f(x)的单调递减区间为
.进而得到f(x)的单调递减区间为 ;单调递增区间为
;单调递增区间为 .即可得到值域.
.即可得到值域.点评:熟练掌握三角函数的图象与性质是解题的关键.

练习册系列答案
相关题目
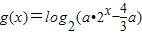 ,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围. ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.